- Forward projections in
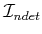 :
:
- Starting from a nondeterministic I-state,
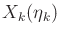 , and
applying an action
, and
applying an action 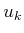 , derive an expression for the
nondeterministic one-stage forward projection by extending the
presentation in Section 10.1.2.
, derive an expression for the
nondeterministic one-stage forward projection by extending the
presentation in Section 10.1.2.
- Determine an expression for the two-stage forward projection
starting from
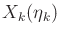 and applying
and applying 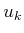 and
and 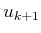 .
.
- Forward projections in
 :
:
- Starting from a probabilistic I-state,
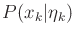 , and
applying an action
, and
applying an action 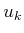 , derive an expression for the probabilistic
one-stage forward projection.
, derive an expression for the probabilistic
one-stage forward projection.
- Determine an expression for the two-stage forward projection
starting from
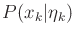 and applying
and applying 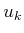 and
and 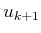 .
.
- Determine the strong and weak backprojections on
 for
a given history I-state,
for
a given history I-state, 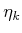 . These should give sets of possible
. These should give sets of possible
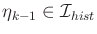 .
.
- At the end of Section 11.3.2, it was mentioned that an
equivalent DFA can be constructed from an NFA.
- Give an explicit DFA that accepts the same set of strings
as the NFA in Figure 11.8b.
- Express the problem of determining whether the NFA in Figure
11.8b accepts any strings as a planning problem
using Formulation 2.1.
- This problem involves computing probabilistic
I-states for Example 11.14. Let the initial I-state be
![$\displaystyle P(x_1) = [ 1/3 \;\; 1/3 \;\; 1/3] ,$](img5008.gif) |
(11.90) |
in which the 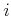 th entry in the vector indicates
th entry in the vector indicates
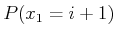 .
Let
.
Let
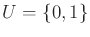 . For each action, a state transition matrix can be
specified, which gives the probabilities
. For each action, a state transition matrix can be
specified, which gives the probabilities
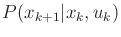 . For
. For  , let
, let
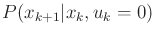 be
be
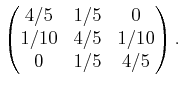 |
(11.91) |
The 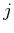 th entry of the
th entry of the 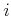 th row yields
th row yields
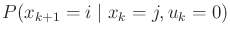 . For
. For 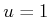 , let
, let
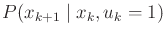 be
be
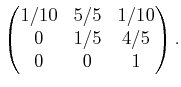 |
(11.92) |
The sensing model is specified by three vectors:
![$\displaystyle P(y_k\vert x_k=0) = [4/5 \;\; 1/5] ,$](img5016.gif) |
(11.93) |
![$\displaystyle P(y_k\vert x_k=1) = [1/2 \;\; 1/2] ,$](img5017.gif) |
(11.94) |
and
![$\displaystyle P(y_k\vert x_k=2) = [1/5 \;\; 4/5] ,$](img5018.gif) |
(11.95) |
in which the 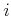 th component yields
th component yields
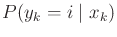 .
Suppose that
.
Suppose that 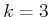 and the history I-state obtained so far is
and the history I-state obtained so far is
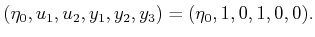 |
(11.96) |
The task is to compute the probabilistic I-state.
Starting from 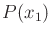 , compute the following
distributions:
, compute the following
distributions:
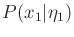 ,
,
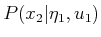 ,
,
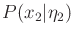 ,
,
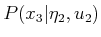 ,
,
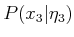 .
.
- Explain why it is not possible to reach every nondeterministic
I-state from every other one for Example 11.7. Give an
example of a nondeterministic I-state that cannot be reached from the
initial I-state. Completely characterize the reachability of
nondeterministic I-states from all possible initial conditions.
Figure 11.33:
(a) A topological graph in which a point
moves (note that two vertices are vertically aligned). (b) An exercise
that is a variant of Example 11.17.
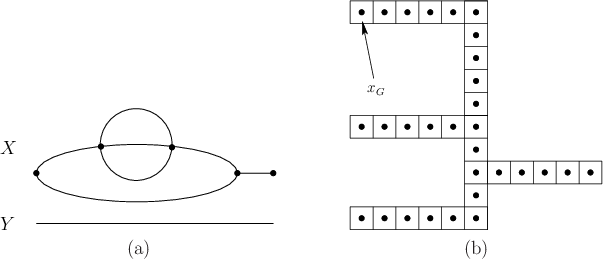 |
- In the same spirit as Example 11.21, consider a
point moving on the topological graph shown in Figure
11.33. Fully characterize the connectivity of
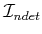 (you may exploit symmetries to simplify the answer).
(you may exploit symmetries to simplify the answer).
- Design an I-map for Example 11.17 that is not
necessarily sufficient but leads to a solution plan defined over only
three derived I-states.
- Consider the discrete problem in Figure 11.33b,
using the same sensing and motion model as in Example 11.17.
- Develop a sufficient I-map and a solution plan that uses as few
derived I-states as possible.
- Develop an I-map that is not necessarily sufficient, and a
solution plan that uses as few derived I-states as possible.
- Suppose that there are two I-maps,
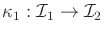 and
and
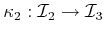 , and it is given
that
, and it is given
that
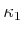 is sufficient with respect to
is sufficient with respect to
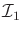 , and
, and
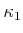 is sufficient with respect to
is sufficient with respect to
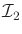 . Determine whether the I-map
. Determine whether the I-map
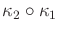 is sufficient with respect to
is sufficient with respect to
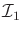 , and
prove your claim.
, and
prove your claim.
- Propose a solution to Example 11.16 that uses fewer
nondeterministic I-states.
- Suppose that a point robot moves in
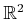 and receives observations from three homing beacons that are not
collinear and originate from known locations. Assume that the robot
can calibrate the three observations on
and receives observations from three homing beacons that are not
collinear and originate from known locations. Assume that the robot
can calibrate the three observations on
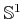 .
.
- Prove that the robot can always recover its position in
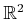 .
.
- What can the robot infer if there are only two beacons?
- Nondeterministic I-state problems:
- Prove that the nondeterministic I-states for Example
11.23 are always a single connected region whose
boundary is composed only of circular arcs and line segments.
- Design an algorithm for efficiently computing the
nondeterministic I-states from stage to stage.
- Design an algorithm that takes as input a simply connected
rectilinear region (i.e., described by a polygon that has all right
angles) and a goal state, and designs a sequence of tray tilts that
guarantees the ball will come to rest at the goal. Example
11.24 provides an illustration.
- Extend the game-theoretic formulation from Section
11.7.2 of history I-spaces to continuous time.
- Consider the ``where did I come from?''
problem.
- Derive an expression for
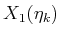 .
.
- Derive an expression for
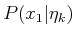 .
.
- In the game of Example 11.27, could there exist a
point in the game at which one player has not yet observed every
possible ``hit'' yet it knows the state of the game (i.e., the exact
location of all ships)? Explain.
- When playing blackjack in casinos, many card-counting
strategies involve remembering simple
statistics of the cards, rather than the entire history of cards seen
so far. Define a game of blackjack and card counting as an example of
history I-states and an I-map that dramatically reduces the size of the
I-space, and an information-feedback plan.
Implementations
- Implement the Kalman filter for the case of a robot moving in
the plane. Show the confidence ellipsoids obtained during execution.
Be careful of numerical issues (see [564]).
- Implement probabilistic I-state computations for a point robot
moving in a 2D polygonal environment. Compare the efficiency and
accuracy of grid-based approximations to particle filtering.
- Design and implement an algorithm that uses nondeterministic
I-states to play a good game of Battleship, as explained in Example
11.27.
Steven M LaValle
2020-08-14

