
Next: Further Reading Up: 11.7 Information Spaces in Previous: 11.7.1 Information States in
I-space concepts can also be incorporated into sequential games that
are played over state spaces. The resulting formulation naturally
extends Formulation 11.1 of Section 11.1 to
multiple players. Rather than starting with two players and
generalizing later, the full generality of having ![]() players is
assumed up front. The focus in this section is primarily on characterizing I-spaces for such games, rather than solving them.
Solution approaches depend heavily on the particular information
models; therefore, they will not be covered here.
players is
assumed up front. The focus in this section is primarily on characterizing I-spaces for such games, rather than solving them.
Solution approaches depend heavily on the particular information
models; therefore, they will not be covered here.
As in Section 11.7.1, each player has its own frame of
reference and therefore its own I-space. The I-state for each player
indicates its information regarding a common game state. This is the
same state as introduced in Section 10.5; however, each
player may have different observations and may not know the actions
of others. Therefore, the I-state is different for each decision
maker. In the case of perfect state sensing, these I-spaces all
collapse to ![]() .
.
Suppose that there are ![]() players. As presented in Section
10.5, each player has its own action space,
players. As presented in Section
10.5, each player has its own action space, ![]() ; however,
here it is not allowed to depend on
; however,
here it is not allowed to depend on ![]() , because the state may
generally be unknown. It can depend, however, on the I-state. If
nature actions may interfere with the state transition equation, then
(10.120) is used (if there are two players);
otherwise, (10.121) is used, which leads to
predictable future states if the actions of all of the players are
given. A single nature action,
, because the state may
generally be unknown. It can depend, however, on the I-state. If
nature actions may interfere with the state transition equation, then
(10.120) is used (if there are two players);
otherwise, (10.121) is used, which leads to
predictable future states if the actions of all of the players are
given. A single nature action,
![]() , is used to model the effect of nature
across all players when uncertainty in prediction exists.
, is used to model the effect of nature
across all players when uncertainty in prediction exists.
Any of the sensor models from Section 11.1.1 may be
defined in the case of multiple players. Each has its own observation
space ![]() and sensor mapping
and sensor mapping ![]() . For each player, nature may
interfere with observations through nature sensing actions,
. For each player, nature may
interfere with observations through nature sensing actions,
![]() . A state-action sensor mapping appears as
. A state-action sensor mapping appears as
![]() ; state sensor mappings and history-based sensor mappings
may also be defined.
; state sensor mappings and history-based sensor mappings
may also be defined.
Consider how the game appears to a single player at stage ![]() . What
information might be available for making a decision? Each player
produces the following in the most general case: 1) an initial
condition,
. What
information might be available for making a decision? Each player
produces the following in the most general case: 1) an initial
condition,
![]() ; 2) an action history,
; 2) an action history,
![]() ; and 3) and
an observation history,
; and 3) and
an observation history,
![]() . It must be specified whether
one player knows the previous actions that have been applied by other
players. It might even be possible for one player to receive the
observations of other players. If
. It must be specified whether
one player knows the previous actions that have been applied by other
players. It might even be possible for one player to receive the
observations of other players. If
![]() receives all of this
information, its history I-state at stage
receives all of this
information, its history I-state at stage ![]() is
is
Assuming all spaces are finite, the concepts given so far can be organized into a sequential game formulation that is the imperfect state information counterpart of Formulation 10.4:
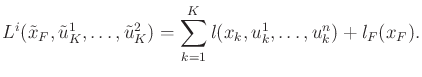 |
(11.89) |
An interesting specialization of Formulation 11.4 is when all players have identical cost functions. This is not equivalent to having a single player because the players have different I-states. For example, a task may be for several robots to search for a treasure, but they have limited communication between them. This results in different I-states. They would all like to cooperate, but they are unable to do so without knowing the state. Such problems fall under the subject of team theory [225,450,530].
As for the games considered in Formulation 10.4, each player has its own plan. Since the players do not necessarily know the state, the decisions are based on the I-state. The definitions of a deterministic plan, a globally randomized plan, and a locally randomized plan are essentially the same as in Section 11.7.1. The only difference is that more general I-spaces are defined in the current setting. Various kinds of solution concepts, such as saddle points and Nash equilibria, can be defined for the general game in Formulation 11.4. The existence of locally randomized saddle points and Nash equilibria depends on general on the particular information model [59].
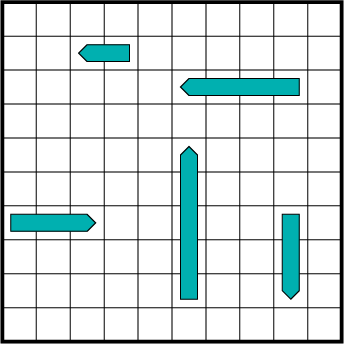 |
A state is the specification of the exact location of all ships on each player's grid. The state space yields the set of all possible ship locations for both players. Each player always knows the location of its own ships. Once they are placed on the grid, they are never allowed to move.
The players take turns guessing a single grid tile, expressed as a row and column, that it suspects contains a ship. The possible observations are ``hit'' and ``miss,'' depending on whether a ship was at that location. In each turn, a single guess is made, and the players continue taking turns until one player has observed a hit for every tile that was occupied by a ship.
This is an interesting game because once a ``hit'' is discovered, it
is clear that a player should search for other hits in the vicinity
because there are going to be several contiguous tiles covered by the
same ship. The only problem is that the precise ship position and
orientation are unknown. A good player essentially uses the
nondeterministic I-state to improve the chances that a hit will occur
next.
![]()
Steven M LaValle 2020-08-14