
Next: 11.5.3 Examples with Nature Up: 11.5 Examples for Continuous Previous: Odometry sensors
This section gives examples of I-spaces for which the sensor mapping
is ![]() and
and ![]() is a projection that reveals some of the state
variables, while concealing others. The examples all involve
continuous time, and the focus is mainly on the nondeterministic
I-space
is a projection that reveals some of the state
variables, while concealing others. The examples all involve
continuous time, and the focus is mainly on the nondeterministic
I-space
![]() . It is assumed that there are no actions, which
means that
. It is assumed that there are no actions, which
means that
![]() . Nature actions,
. Nature actions, ![]() , however,
will be allowed. Since there are no robot actions and no nature
sensing actions, all of the uncertainty arises from the fact that
, however,
will be allowed. Since there are no robot actions and no nature
sensing actions, all of the uncertainty arises from the fact that ![]() is a projection and the nature actions that affect the state
transition equation are not known. This is a very important and
interesting class of problems in itself. The examples can be further
complicated by allowing some control from the action set,
is a projection and the nature actions that affect the state
transition equation are not known. This is a very important and
interesting class of problems in itself. The examples can be further
complicated by allowing some control from the action set, ![]() ;
however, the purpose here is to illustrate I-space concepts.
Therefore, it will not be necessary.
;
however, the purpose here is to illustrate I-space concepts.
Therefore, it will not be necessary.
| (11.72) |
The nature action space is
![]() , in which
, in which ![]() means to
move at unit speed in the
means to
move at unit speed in the ![]() direction along the sine curve, and
direction along the sine curve, and
![]() means to move at unit speed in the
means to move at unit speed in the ![]() direction along the
curve. Thus, for some nature action history
direction along the
curve. Thus, for some nature action history
![]() , a state
trajectory
, a state
trajectory
![]() that moves the point along the curve can be
determined by integration.
that moves the point along the curve can be
determined by integration.
A history I-state takes the form
![]() , which
includes the initial condition
, which
includes the initial condition
![]() and the observation
history
and the observation
history
![]() up to time
up to time ![]() . The nondeterministic I-states are
very interesting for this problem. For each observation
. The nondeterministic I-states are
very interesting for this problem. For each observation ![]() , the
preimage
, the
preimage ![]() is a countably infinite set of points that
corresponds to the intersection of
is a countably infinite set of points that
corresponds to the intersection of ![]() with a horizontal line at
height
with a horizontal line at
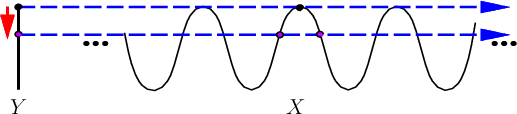
height ![]() , as shown in Figure 11.18.
, as shown in Figure 11.18.
The uncertainty for this problem is always characterized by the number
of intersection points that might contain the true state. Suppose
that ![]() . In this case, there is no state trajectory that can
reduce the amount of uncertainty. As the point moves along
. In this case, there is no state trajectory that can
reduce the amount of uncertainty. As the point moves along ![]() , the
height is always known because of the sensor, but the
, the
height is always known because of the sensor, but the ![]() coordinate
can only be narrowed down to being any of the intersection points.
coordinate
can only be narrowed down to being any of the intersection points.
 |
Suppose instead that
![]() , in which
, in which ![]() is some
particular point along
is some
particular point along ![]() . If
. If ![]() remains within
remains within ![]() over some
any period of time starting at
over some
any period of time starting at ![]() , then
, then ![]() is known because
the exact segment of the sine curve that contains the state is known.
However, if the point reaches an extremum, which results in
is known because
the exact segment of the sine curve that contains the state is known.
However, if the point reaches an extremum, which results in ![]() or
or
![]() , then it is not known which way the point will travel. From
this point, the sensor cannot disambiguate moving in the
, then it is not known which way the point will travel. From
this point, the sensor cannot disambiguate moving in the ![]() direction from the
direction from the ![]() direction. Therefore, the uncertainty grows,
as shown in Figure 11.19. After the observation
direction. Therefore, the uncertainty grows,
as shown in Figure 11.19. After the observation ![]() is
obtained, there are two possibilities for the current state, depending
on which action was taken by nature when
is
obtained, there are two possibilities for the current state, depending
on which action was taken by nature when ![]() ; hence, the
nondeterministic I-state contains two states. If the motion continues
until
; hence, the
nondeterministic I-state contains two states. If the motion continues
until ![]() , then there will be four states in the nondeterministic
I-state. Unfortunately, the uncertainty can only grow in this
example. There is no way to use the sensor to reduce the size of the
nondeterministic I-states.
, then there will be four states in the nondeterministic
I-state. Unfortunately, the uncertainty can only grow in this
example. There is no way to use the sensor to reduce the size of the
nondeterministic I-states.
![]()
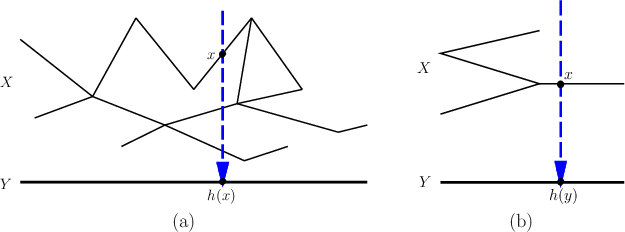 |
The previous example can be generalized to observing a single
coordinate of a point that moves around in a planar topological graph,
as shown in Figure 11.20a. Most of the model remains the
same as for Example 11.20, except that the state space is now
a graph. The set of nature actions, ![]() , needs to be extended
so that if
, needs to be extended
so that if ![]() is a vertex of the graph, then there is one input for
each incident edge. These are the possible directions along which the
point could move.
is a vertex of the graph, then there is one input for
each incident edge. These are the possible directions along which the
point could move.
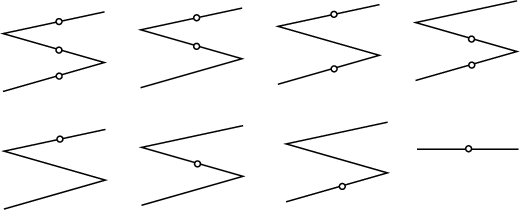 |
The eight pieces of
![]() depicted in Figure 11.21
are connected together in an interesting way. Suppose that the point
is on the rightmost edge and moves left. After crossing the vertex,
the I-state must be the case shown in the upper right of Figure
11.21, which indicates that the point could be on one of
two edges. If the point travels right from one of the I-states of the
left edges, then the I-state shown in the bottom right of Figure
11.20 is always reached; however, it is not necessarily
possible to return to the same I-state on the left. Thus, in general,
there are directional constraints on
depicted in Figure 11.21
are connected together in an interesting way. Suppose that the point
is on the rightmost edge and moves left. After crossing the vertex,
the I-state must be the case shown in the upper right of Figure
11.21, which indicates that the point could be on one of
two edges. If the point travels right from one of the I-states of the
left edges, then the I-state shown in the bottom right of Figure
11.20 is always reached; however, it is not necessarily
possible to return to the same I-state on the left. Thus, in general,
there are directional constraints on
![]() . Also, note that from
the I-state on the lower left of Figure 11.20, it is
impossible to reach the I-state on the lower right by moving straight
right. This is because it is known from the structure of the graph
that this is impossible.
. Also, note that from
the I-state on the lower left of Figure 11.20, it is
impossible to reach the I-state on the lower right by moving straight
right. This is because it is known from the structure of the graph
that this is impossible.
![]()
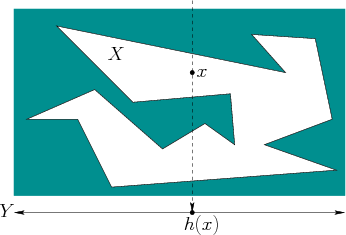 |
The graph example can be generalized substantially to reflect a wide variety of problems that occur in robotics and other areas. For example, Figure 11.22 shows a polygon in which a point can move. Only one coordinate is observed, and the resulting nondeterministic I-space has layers similar to those obtained for Example 11.21. These ideas can be generalized to any dimension. Interesting models can be constructed using the simple projection sensors, such as a position sensor or compass, from Section 11.5.1. In Section 12.4, such layers will appear in a pursuit-evasion game that uses visibility sensors to find moving targets.
Steven M LaValle 2020-08-14