2.1.1 Problem Formulation

The discrete feasible planning model will be defined using state-space models, which will appear repeatedly throughout this book. Most of these will be natural extensions of the model presented in this section. The basic idea is that each distinct situation for the world is called a state, denoted by $x$, and the set of all possible states is called a state space, $X$. For discrete planning, it will be important that this set is countable; in most cases it will be finite. In a given application, the state space should be defined carefully so that irrelevant information is not encoded into a state (e.g., a planning problem that involves moving a robot in France should not encode information about whether certain light bulbs are on in China). The inclusion of irrelevant information can easily convert a problem that is amenable to efficient algorithmic solutions into one that is intractable. On the other hand, it is important that $X$ is large enough to include all information that is relevant to solve the task.

The world may be transformed through the application of actions that are chosen by the planner. Each action, $u$, when applied from the current state, $x$, produces a new state, $x'$, as specified by a state transition function, $f$. It is convenient to use $f$ to express a state transition equation,

$$x' = f(x,u) .$$ (2.1)

Let $U(x)$ denote the action space for each state $x$, which represents the set of all actions that could be applied from $x$. For distinct $x,x' \in X$, $U(x)$ and $U(x')$ are not necessarily disjoint; the same action may be applicable in multiple states. Therefore, it is convenient to define the set $U$ of all possible actions over all states:

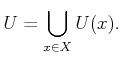$$U = \bigcup_{x \in X} U(x) .$$ (2.2)

As part of the planning problem, a set ${X_{G}}\subset X$ of goal states is defined. The task of a planning algorithm is to find a finite sequence of actions that when applied, transforms the initial state ${x_{I}}$ to some state in ${X_{G}}$. The model is summarized as:

Formulation 2..1 (Discrete Feasible Planning)  

1. A nonempty state space $X$, which is a finite or countably infinite set of states.
2. For each state $x \in X$, a finite action space $U(x)$.
3. A state transition function $f$ that produces a state $f(x,u) \in X$ for every $x \in X$ and ${ u}\in U(x)$. The state transition equation is derived from $f$ as $x' = f(x,u)$.
4. An initial state ${x_{I}}\in X$.
5. A goal set ${X_{G}}\subset X$.

It is often convenient to express Formulation 2.1 as a directed state transition graph. The set of vertices is the state space $X$. A directed edge from $x \in X$ to $x' \in X$ exists in the graph if and only if there exists an action $u \in U(x)$ such that $x' = f(x,u)$. The initial state and goal set are designated as special vertices in the graph, which completes the representation of Formulation 2.1 in graph form.