- Suppose that a very fast path planning algorithm runs on board
of a mobile robot (for example, it may find an answer in a few
milliseconds, which is reasonable using trapezoidal decomposition in
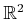 ). Explain how this method can be used to simulate having a
feedback plan on the robot. Explain the issues and trade-offs between
having a fast on-line algorithm that computes open-loop plans vs. a
better off-line algorithm that computes a feedback plan.
). Explain how this method can be used to simulate having a
feedback plan on the robot. Explain the issues and trade-offs between
having a fast on-line algorithm that computes open-loop plans vs. a
better off-line algorithm that computes a feedback plan.
- Use Dijkstra's algorithm to construct navigation functions on a
2D grid with obstacles. Experiment with adding a penalty to the cost
functional for getting too close to obstacles.
- If there are alternative routes, the NF2
algorithm does not necessarily send the state along the route that has
the largest maximum clearance. Fix the NF2 algorithm so that it
addresses this problem.
- Tangent space problems:
- For the manifold of unit quaternions, find basis vectors for the
tangent space in
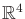 at any point.
at any point.
- Find basis vectors for the tangent space in
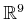 , assuming
that matrices in
, assuming
that matrices in 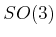 are parameterized with quaternions, as shown
in (4.20).
are parameterized with quaternions, as shown
in (4.20).
- Extend the algorithm described in Section 8.4.3 to
make it work for polygons that have holes. See Example
8.16 for a similar problem.
- Give a complete algorithm that uses the vertical cell
decomposition for a polygonal obstacle region in
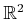 to construct
a vector field that serves as a feedback plan. The vector field may
be discontinuous.
to construct
a vector field that serves as a feedback plan. The vector field may
be discontinuous.
Figure 8.23:
Consider designing a continuous vector
field that flows into 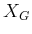 .
.
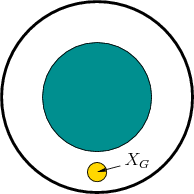 |
- Figure 8.23 depicts a 2D example for which
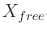 is an open annulus. Consider designing a vector field for which all
integral curves flow into
is an open annulus. Consider designing a vector field for which all
integral curves flow into 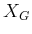 and the vector field is continuous
outside of
and the vector field is continuous
outside of 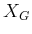 . Either give a vector field that achieves this
or explain why it is not possible.
. Either give a vector field that achieves this
or explain why it is not possible.
- Use the maximum-clearance roadmap idea from Section
6.2.3 to define a cell decomposition and feedback motion
plan (vector field) that maximizes clearance. The vector field may be
discontinuous.
- Develop an algorithm that computes an exact cover for a
polygonal configuration space and ensures that if two neighborhoods
intersect, then their intersection always contains an open set (i.e.,
the overlap region is two-dimensional). The neighborhoods in the
cover should be polygonal.
- Using a distance measurement and Euler angles, determine the
expression for a collision-free ball that can be inferred (make the
ball as large as possible). This should generalize
(8.54).
- Using a distance measurement and quaternions, determine the
expression for a collision-free ball (once again, make it as large as
possible).
- Generalize the multi-linear interpolation
scheme in (8.59) from
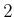 to
to 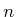 dimensions.
dimensions.
- Explain the convergence problems for value iteration that can
result if
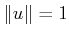 is used to constraint the set of allowable
actions, instead of
is used to constraint the set of allowable
actions, instead of
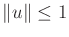 .
.
Implementations
- Experiment with numerical methods for solving the function
(8.49) in two dimensions under various boundary
conditions. Report on the efficiency and accuracy of the methods.
How well can they be applied in higher dimensions?
- Implement value iteration with interpolation (it is not
necessary to use the method in Figure 8.20) for a
polygonal robot that translates and rotates among polygonal obstacles
in
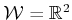 . Define the cost functional so that the distance
traveled is obtained with respect to a weighted Euclidean metric (the
weights that compare rotation to translation can be set arbitrarily).
. Define the cost functional so that the distance
traveled is obtained with respect to a weighted Euclidean metric (the
weights that compare rotation to translation can be set arbitrarily).
- Evaluate the efficiency of the interpolation method shown in
Figure 8.20 applied to multi-linear interpolation given
by generalizing (8.59) as in Exercise
12. You do not need to implement the full value
iteration approach (alternatively, this could be done, which provides
a better comparison of the overall performance).
- Implement the method of Section 8.4.2 of computing
vector fields on a triangulation. For given input polygons, have your
program draw a needle diagram of the computed vector field. Determine
how fast the vector field can be recomputed as the goal changes.
- Optimal navigation function problems:
- Implement the algorithm illustrated in Figure 8.13.
Show the level sets of the optimal cost-to-go function.
- Extend the algorithm and implementation to the case in which
there are polygonal holes in
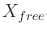 .
.
- Adapt value iteration with interpolation so that a point robot
moving in the plane can keep track of a predictable moving point
called a target. The cost functional should cause a small
penalty to be added if the target is not visible. Optimizing this
should minimize the amount of time that the target is not visible.
Assume that the initial configuration of the robot is given. Compute
optimal feedback plans for the robot.
- Try to experimentally construct navigation functions by adding
potential functions that repel the state away from obstacles and
attract the state toward
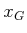 . For simplicity, you may assume
that
. For simplicity, you may assume
that
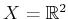 and the obstacles are discs. Start with a single
disc and then gradually construct more complicated obstacle regions.
How difficult is it to ensure that the resulting potential function
has no local minima outside of
and the obstacles are discs. Start with a single
disc and then gradually construct more complicated obstacle regions.
How difficult is it to ensure that the resulting potential function
has no local minima outside of 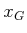 ?
?
Steven M LaValle
2020-08-14
