8.4.3 Optimal Navigation Functions

The vector fields developed in the last section yield feasible trajectories, but not necessarily optimal trajectories unless the initial and goal states are in the same convex $n$-cell. If $X = {\mathbb{R}}^2$, then it is possible to make a continuous version of Dijkstra's algorithm [708]. This results in an exact cost-to-go function over $X$ based on the Euclidean shortest path to a goal, ${x_{G}}$. The cost-to-go function serves as the navigation function, from which the feedback plan is defined by using a local steepest descent.

Suppose that $X$ is bounded by a simple polygon (no holes). Assume that only normalized vector fields are allowed. The cost functional is assumed to be the Euclidean distance traveled along a state trajectory. Recall from Section 6.2.4 that for optimal path planning, $X = \operatorname{cl}({\cal C}_{free})$ must be used. Assume that ${\cal C}_{free}$ and $\operatorname{cl}({\cal C}_{free})$ have the same connectivity.^8.12 This technically interferes with the definition of tangent spaces from Section 8.3 because each point of $X$ must be contained in an open neighborhood. Nevertheless, we allow vectors along the boundary, provided that they ``point'' in a direction tangent to the boundary. This can be formally defined by considering boundary regions as separate manifolds.

Figure 8.12: (a) A point, $x$, in a simple polygon. (b) The visibility polygon, $V(x)$.

Figure 8.13: The optimal navigation function is computed in four iterations. In each iteration, the navigation function is extended from a new way point.

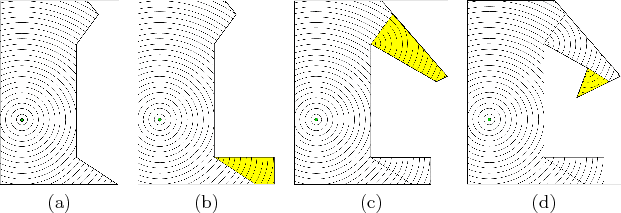Consider computing the optimal cost-to-go to a point ${x_{G}}$ for a problem such as that shown in Figure 8.12a. For any $x \in X$, let the visibility polygon $V(x)$ refer to the set of all points visible from $x$, which is illustrated in Figure 8.12b. A point $x'$ lies in $V(x)$ if and only if the line segment from $x'$ to $x$ is contained in $X$. This implies that the cost-to-go from $x'$ to $x$ is just the Euclidean distance from $x'$ to $x$. The optimal navigation function can therefore be immediately defined over $V({x_{G}})$ as

$$\phi(x) = \Vert x-{x_{G}}\Vert .$$ (8.42)

Level sets at regularly spaced values of this navigation function are shown in Figure 8.13a.

How do we compute the optimal cost-to-go values for the points in $X \setminus V({x_{G}})$? For the segments on the boundary of $V(x)$ for any $x \in X$, some edges are contained in the boundary of $X$, and others cross the interior of $X$. For the example in Figure 8.12b, there are two edges that cross the interior. For each segment that crosses the interior, let the closer of the two vertices to $x$ be referred to as a way point. Two way points are indicated in Figure 8.12b. The way points of $V({x_{G}})$ are places through which some optimal paths must cross. Let $W(x)$ for any $x \in X$ denote the set of way points of $V(x)$.

A straightforward algorithm proceeds as follows. Let $Z_i$ denote the set of points over which $\phi$ has been defined, in the $i$th iteration of the algorithm. In the first iteration, $Z_1 = V({x_{G}})$, which is the case shown in Figure 8.13a. The way points of $V({x_{G}})$ are placed in a queue, $Q$. In each following iteration, a way point $x$ is removed from $Q$. Let $Z_i$ denote the domain over which $\phi$ is defined so far. The domain of $\phi$ is extended to include all new points visible from $x$. These new points are $V(x) \setminus Z_i$. This yields $Z_{i+1} = Z_i \cup V(x)$, the extended domain of $\phi$. The values of $\phi(x')$ for $x' \in Z_{i+1} \setminus Z_i$ are defined by

$$\phi(x') = \phi(x) + \Vert x'-x\Vert ,$$ (8.43)

in which $x$ is the way point that was removed from $Q$ (the optimal cost-to-go value of $x$ was already computed). The way points of $V(x)$ that do not lie in $Z_{i+1}$ are added to $Q$. Each of these will yield new portions of $X$ that have not yet been seen. The algorithm terminates when $Q$ is empty, which implies that $Z_k = X$ for some $k$. The execution of the algorithm is illustrated in Figure 8.13.

The visibility polygon can be computed in time $O(n \lg n)$ if $X$ is described by $n$ edges. This is accomplished by performing a radial sweep, which is an adaptation of the method applied in Section 6.2.2 for vertical cell decomposition. The difference for computing $V(x)$ is that a ray anchored at $x$ is swept radially (like a radar sweep). The segments that intersect the ray are sorted by their distance from $x$. For the algorithm that constructs the navigation function, no more than $O(n)$ visibility polygons are computed because each one is computed from a unique way point. This implies $O(n^2 \lg n)$ running time for the whole algorithm. Unfortunately, there is no extension to higher dimensions; recall from Section 7.7.1 that computing shortest paths in a 3D environment is NP-hard [172].

The algorithm given here is easy to describe, but it is not the most general, nor the most efficient. If $X$ has holes, then the level set curves can collide by arriving from different directions when traveling around an obstacle. The queue, $Q$, described above can be sorted as in Dijkstra's algorithm, and special data structures are needed to identify when critical events occur as the cost-to-go is propagated outward. It was shown in [443] that this can be done in time $O(n \lg n)$ and space $O(n \lg n)$.