6.2.2 Vertical Cell Decomposition
Cell decompositions will be defined formally in Section
6.3, but here we use the notion informally.
Combinatorial methods must construct a finite data structure that
exactly encodes the planning problem. Cell decomposition algorithms
achieve this partitioning of
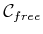 into a finite set of regions called
cells. The term
into a finite set of regions called
cells. The term 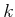 -cell refers to a
-cell refers to a
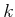 -dimensional cell. The cell decomposition should satisfy three
properties:
-dimensional cell. The cell decomposition should satisfy three
properties:
- Computing a path from one point to another inside of a cell must
be trivially easy. For example, if every cell is convex, then any pair
of points in a cell can be connected by a line segment.
- Adjacency information for the cells can be easily extracted to
build the roadmap.
- For a given
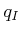 and
and 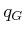 , it should be efficient to
determine which cells contain them.
, it should be efficient to
determine which cells contain them.
If a cell decomposition satisfies these properties, then the motion
planning problem is reduced to a graph search problem. Once again the
algorithms of Section 2.2 may be applied; however, in the
current setting, the entire graph, 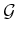 , is usually known in
advance.6.3 This was not assumed
for discrete planning problems.
, is usually known in
advance.6.3 This was not assumed
for discrete planning problems.
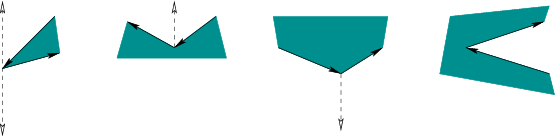
Figure 6.2:
There are four general cases: 1)
extending upward and downward, 2) upward only, 3) downward only, and
4) no possible extension.
 |
Subsections
Steven M LaValle
2020-08-14

![]() into a finite set of regions called
cells. The term
into a finite set of regions called
cells. The term ![]() -cell refers to a
-cell refers to a
![]() -dimensional cell. The cell decomposition should satisfy three
properties:
-dimensional cell. The cell decomposition should satisfy three
properties:
