Another important family of navigation functions is constructed from
harmonic functions [236,239,240,481,529]. A
function 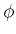 is called a harmonic function if it satisfies
the differential equation
is called a harmonic function if it satisfies
the differential equation
 |
(8.49) |
There are many possible solutions to the equation, depending on the
conditions along the boundary of the domain over which 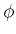 is
defined. A simple disc-based example is given in [235]
for which an analytical solution exists. Complicated navigation
functions are generally defined by imposing constraints on
is
defined. A simple disc-based example is given in [235]
for which an analytical solution exists. Complicated navigation
functions are generally defined by imposing constraints on 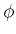 along the boundary of
along the boundary of
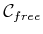 . A Dirichlet boundary condition
means that the boundary must be held to a constant value. Using this
condition, a harmonic navigation function can be developed that guides
the state into a goal region from anywhere in a simply connected state
space. If there are interior obstacles, then a Neumann boundary
condition forces the velocity vectors to be tangent to the obstacle
boundary. By solving (8.49) under a combination of both
boundary conditions, a harmonic navigation function can be constructed
that avoids obstacles by moving parallel to their boundaries and
eventually landing in the goal. It has been shown under general
conditions that navigation functions can be produced
[240,239]; however, the main problems are that the
boundary of
. A Dirichlet boundary condition
means that the boundary must be held to a constant value. Using this
condition, a harmonic navigation function can be developed that guides
the state into a goal region from anywhere in a simply connected state
space. If there are interior obstacles, then a Neumann boundary
condition forces the velocity vectors to be tangent to the obstacle
boundary. By solving (8.49) under a combination of both
boundary conditions, a harmonic navigation function can be constructed
that avoids obstacles by moving parallel to their boundaries and
eventually landing in the goal. It has been shown under general
conditions that navigation functions can be produced
[240,239]; however, the main problems are that the
boundary of
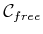 is usually not constructed explicitly (recall why
this was avoided in Chapter 5) and that a numerical
solution to (8.49) is expensive to compute. This can be
achieved, for example, by using Gauss-Seidel iterations (as indicated
in [240]), which are related to value iteration (see
[96] for the distinction). A sampling-based approach to
constructing navigation functions via harmonic functions is presented
in [124]. Value iteration will be used to produce approximate,
optimal navigation functions in Section 8.5.2.
is usually not constructed explicitly (recall why
this was avoided in Chapter 5) and that a numerical
solution to (8.49) is expensive to compute. This can be
achieved, for example, by using Gauss-Seidel iterations (as indicated
in [240]), which are related to value iteration (see
[96] for the distinction). A sampling-based approach to
constructing navigation functions via harmonic functions is presented
in [124]. Value iteration will be used to produce approximate,
optimal navigation functions in Section 8.5.2.
Steven M LaValle
2020-08-14

![]() is called a harmonic function if it satisfies
the differential equation
is called a harmonic function if it satisfies
the differential equation