For defining new neighborhoods, it is important to keep them simple
because during execution, the neighborhoods that contain the state 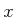 must be determined quickly. Suppose that all neighborhoods are open
balls:
must be determined quickly. Suppose that all neighborhoods are open
balls:
 |
(8.52) |
in which 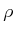 is the metric on
is the metric on 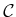 . There are efficient algorithms
for determining whether
. There are efficient algorithms
for determining whether  for some
for some
 , assuming all of
the neighborhoods are balls [700]. In practice,
methods based on Kd-trees yield good performance
[47,52] (recall Section 5.5.2). A new
ball,
, assuming all of
the neighborhoods are balls [700]. In practice,
methods based on Kd-trees yield good performance
[47,52] (recall Section 5.5.2). A new
ball,  , can be constructed in Step 3 for
, can be constructed in Step 3 for
 , but what radius can be assigned? For a point robot that
translates in
, but what radius can be assigned? For a point robot that
translates in
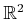 or
or
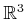 , the Hausdorff distance
, the Hausdorff distance 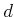 between
the robot and obstacles in
between
the robot and obstacles in 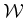 is precisely the distance to
is precisely the distance to
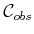 from
from
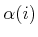 . This implies that we can set
. This implies that we can set  , and
, and  is guaranteed to be collision-free.
is guaranteed to be collision-free.
In a general configuration space, it is possible to find a value of
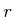 such that
such that
 , but in general
, but in general  . This
issue arose in Section 5.3.4 for checking path segments.
The transformations of Sections 3.2 and 3.3
become important in the determination of
. This
issue arose in Section 5.3.4 for checking path segments.
The transformations of Sections 3.2 and 3.3
become important in the determination of 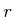 . For illustrative
purposes, suppose that
. For illustrative
purposes, suppose that
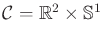 , which corresponds to
a rigid robot,
, which corresponds to
a rigid robot, 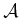 , that can translate and rotate in
, that can translate and rotate in
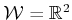 .
Each point
.
Each point
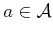 is transformed using (3.35). Now
imagine starting with some configuration
is transformed using (3.35). Now
imagine starting with some configuration
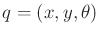 and
perturbing each coordinate by some
and
perturbing each coordinate by some  ,
,  , and
, and
 . What is the maximum distance that a point on
. What is the maximum distance that a point on 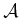 could
travel? Translation affects all points on
could
travel? Translation affects all points on 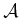 the same way, but
rotation affects points differently. Recall Figure
5.12 from Section 5.3.4. Let
the same way, but
rotation affects points differently. Recall Figure
5.12 from Section 5.3.4. Let
 denote the point that is furthest from the origin
denote the point that is furthest from the origin 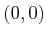 . Let
. Let
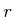 denote the distance from
denote the distance from 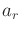 to the origin. If the rotation is
perturbed by some small amount,
to the origin. If the rotation is
perturbed by some small amount,
 , then the displacement
of any
, then the displacement
of any
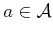 is no more than
is no more than
 . If all three
configuration parameters are perturbed, then
. If all three
configuration parameters are perturbed, then
 |
(8.53) |
is the constraint that must be satisfied to ensure that the resulting
ball is contained in
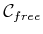 . This is actually the equation of a
solid ellipsoid, which becomes a ball if
. This is actually the equation of a
solid ellipsoid, which becomes a ball if 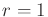 . This can be made
into a ball by reparameterizing
. This can be made
into a ball by reparameterizing 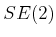 so that
so that
 has
the same affect as
has
the same affect as  and
and  . A transformation
. A transformation
 maps
maps 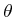 into a new domain
into a new domain
 . In this new space, the equation of the ball is
. In this new space, the equation of the ball is
 |
(8.54) |
in which  represents the change in
represents the change in  . The
reparameterized version of (3.35) is
. The
reparameterized version of (3.35) is
 |
(8.55) |
For a 3D rigid body, similar reparameterizations can be made to Euler
angles or quaternions to generate six-dimensional balls. Extensions
can be made to chains of bodies [983]. One of the main
difficulties, however, is that the balls are not the largest possible.
In higher dimensions the problem becomes worse because numerous balls
are needed, and the radii constructed as described above tend to be
much smaller than what is possible. The number of balls can be
reduced by also allowing axis-aligned cylinders, but it still remains
difficult to construct a cover over a large fraction of
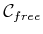 in
more than six dimensions.
in
more than six dimensions.
Steven M LaValle
2020-08-14

![]() must be determined quickly. Suppose that all neighborhoods are open
balls:
must be determined quickly. Suppose that all neighborhoods are open
balls:
![]() such that
such that
![]() , but in general
, but in general ![]() . This
issue arose in Section 5.3.4 for checking path segments.
The transformations of Sections 3.2 and 3.3
become important in the determination of
. This
issue arose in Section 5.3.4 for checking path segments.
The transformations of Sections 3.2 and 3.3
become important in the determination of ![]() . For illustrative
purposes, suppose that
. For illustrative
purposes, suppose that
![]() , which corresponds to
a rigid robot,
, which corresponds to
a rigid robot, ![]() , that can translate and rotate in
, that can translate and rotate in
![]() .
Each point
.
Each point
![]() is transformed using (3.35). Now
imagine starting with some configuration
is transformed using (3.35). Now
imagine starting with some configuration
![]() and
perturbing each coordinate by some
and
perturbing each coordinate by some ![]() ,
, ![]() , and
, and
![]() . What is the maximum distance that a point on
. What is the maximum distance that a point on ![]() could
travel? Translation affects all points on
could
travel? Translation affects all points on ![]() the same way, but
rotation affects points differently. Recall Figure
5.12 from Section 5.3.4. Let
the same way, but
rotation affects points differently. Recall Figure
5.12 from Section 5.3.4. Let
![]() denote the point that is furthest from the origin
denote the point that is furthest from the origin ![]() . Let
. Let
![]() denote the distance from
denote the distance from ![]() to the origin. If the rotation is
perturbed by some small amount,
to the origin. If the rotation is
perturbed by some small amount,
![]() , then the displacement
of any
, then the displacement
of any
![]() is no more than
is no more than
![]() . If all three
configuration parameters are perturbed, then
. If all three
configuration parameters are perturbed, then