
Next: 5.4 Incremental Sampling and Up: 5.3 Collision Detection Previous: 5.3.3 Incremental Methods
Collision detection algorithms determine whether a configuration lies
in
![]() , but motion planning algorithms require that an entire
path maps into
, but motion planning algorithms require that an entire
path maps into
![]() . The interface between the planner and
collision detection usually involves validation of a path segment
(i.e., a path, but often a short one). This cannot be checked
point-by-point because it would require an uncountably infinite number
of calls to the collision detection algorithm.
. The interface between the planner and
collision detection usually involves validation of a path segment
(i.e., a path, but often a short one). This cannot be checked
point-by-point because it would require an uncountably infinite number
of calls to the collision detection algorithm.
Suppose that a path,
![]() , needs to be checked
to determine whether
, needs to be checked
to determine whether
![]() . A common approach
is to sample the interval
. A common approach
is to sample the interval ![]() and call the collision checker only
on the samples. What resolution of sampling is required? How can one
ever guarantee that the places where the path is not sampled are
collision-free? There are both practical and theoretical answers to
these questions. In practice, a fixed
and call the collision checker only
on the samples. What resolution of sampling is required? How can one
ever guarantee that the places where the path is not sampled are
collision-free? There are both practical and theoretical answers to
these questions. In practice, a fixed
![]() is often chosen
as the C-space step size. Points
is often chosen
as the C-space step size. Points
![]() are
then chosen close enough together to ensure that
are
then chosen close enough together to ensure that
![]() , in which
, in which ![]() is the
metric on
is the
metric on ![]() . The value of
. The value of ![]() is often determined
experimentally. If
is often determined
experimentally. If ![]() is too small, then considerable time is
wasted on collision checking. If
is too small, then considerable time is
wasted on collision checking. If ![]() is too large, then there
is a chance that the robot could jump through a thin obstacle.
is too large, then there
is a chance that the robot could jump through a thin obstacle.
Setting ![]() empirically might not seem satisfying.
Fortunately, there are sound algorithmic ways to verify that a path is
collision-free. In some applications the methods are still not used
because they are trickier to implement and they often yield worse
performance. Therefore, both methods are presented here, and you can
decide which is appropriate, depending on the context and your
personal tastes.
empirically might not seem satisfying.
Fortunately, there are sound algorithmic ways to verify that a path is
collision-free. In some applications the methods are still not used
because they are trickier to implement and they often yield worse
performance. Therefore, both methods are presented here, and you can
decide which is appropriate, depending on the context and your
personal tastes.
Ensuring that
![]() requires the use of both
distance information and bounds on the distance that points on
requires the use of both
distance information and bounds on the distance that points on ![]() can travel in
can travel in
![]() . Such bounds can be obtained by using the robot
displacement metric from Example 5.6. Before
expressing the general case, first we will explain the concept in
terms of a rigid robot that translates and rotates in
. Such bounds can be obtained by using the robot
displacement metric from Example 5.6. Before
expressing the general case, first we will explain the concept in
terms of a rigid robot that translates and rotates in
![]() .
Let
.
Let
![]() and
and
![]() . Suppose that
a collision detection algorithm indicates that
. Suppose that
a collision detection algorithm indicates that
![]() is at least
is at least ![]() units away from collision with obstacles in
units away from collision with obstacles in ![]() . This information
can be used to determine a region in
. This information
can be used to determine a region in
![]() that contains
that contains ![]() .
Suppose that the next candidate configuration to be checked along
.
Suppose that the next candidate configuration to be checked along
![]() is
is ![]() . If no point on
. If no point on ![]() travels more than distance
travels more than distance
![]() when moving from
when moving from ![]() to
to ![]() along
along ![]() , then
, then ![]() and all configurations between
and all configurations between ![]() and
and ![]() must be
collision-free. This assumes that on the path from
must be
collision-free. This assumes that on the path from ![]() to
to ![]() ,
every visited configuration must lie between
,
every visited configuration must lie between ![]() and
and ![]() for the
for the
![]() th coordinate and any
th coordinate and any ![]() from
from ![]() to
to ![]() . If the robot can
instead take any path between
. If the robot can
instead take any path between ![]() and
and ![]() , then no such
guarantee can be made).
, then no such
guarantee can be made).
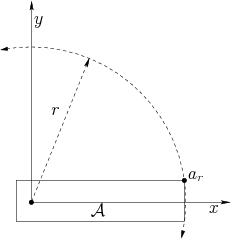 |
When ![]() undergoes a translation, all points move the same distance.
For rotation, however, the distance traveled depends on how far the
point on
undergoes a translation, all points move the same distance.
For rotation, however, the distance traveled depends on how far the
point on ![]() is from the rotation center,
is from the rotation center, ![]() . Let
. Let
![]() denote the point on
denote the point on ![]() that has the largest magnitude,
that has the largest magnitude,
![]() . Figure 5.12 shows an example.
A transformed point
. Figure 5.12 shows an example.
A transformed point
![]() may be denoted by
may be denoted by
![]() . The following bound is obtained for any
. The following bound is obtained for any
![]() , if the robot is rotated from orientation
, if the robot is rotated from orientation ![]() to
to
![]() :
:
| (5.30) |
Similarly, ![]() and
and ![]() may individually vary up to
may individually vary up to ![]() , yielding
, yielding
![]() and
and
![]() . If all three
parameters vary simultaneously, then a region in
. If all three
parameters vary simultaneously, then a region in
![]() can be
defined as
can be
defined as
For the case of ![]() , once again the displacement of the point on
, once again the displacement of the point on
![]() that has the largest magnitude can be bounded. It is best in
this case to express the bounds in terms of quaternion differences,
that has the largest magnitude can be bounded. It is best in
this case to express the bounds in terms of quaternion differences,
![]() . Euler angles may also be used to obtain a
straightforward generalization of (5.31) that has
six terms, three for translation and three for rotation. For each of
the three rotation parts, a point with the largest magnitude in the plane
perpendicular to the rotation axis must be chosen.
. Euler angles may also be used to obtain a
straightforward generalization of (5.31) that has
six terms, three for translation and three for rotation. For each of
the three rotation parts, a point with the largest magnitude in the plane
perpendicular to the rotation axis must be chosen.
If there are multiple links, it becomes much more complicated to
determine the step size. Each point
![]() is transformed by
some nonlinear function based on the kinematic expressions from
Sections 3.3 and 3.4. Let
is transformed by
some nonlinear function based on the kinematic expressions from
Sections 3.3 and 3.4. Let
![]() denote this transformation. In some cases, it might
be possible to derive a Lipschitz condition of the form
denote this transformation. In some cases, it might
be possible to derive a Lipschitz condition of the form
| (5.32) |
A better method is to individually bound the link displacement with respect to each parameter,
| (5.33) |
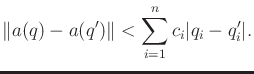 |
(5.34) |
Unfortunately, there are more complications. Suppose the 50-link
chain is in a configuration that folds all of the links on top of each
other (
![]() for each
for each
![]() ). In this case,
). In this case,
![]() does not move as fast when
does not move as fast when ![]() is perturbed, in
comparison to the straight-line configuration. A larger step size for
is perturbed, in
comparison to the straight-line configuration. A larger step size for
![]() could be used for this configuration, relative to other
parts of
could be used for this configuration, relative to other
parts of ![]() . The implication is that, although Lipschitz constants
can be made to hold over all of
. The implication is that, although Lipschitz constants
can be made to hold over all of ![]() , it might be preferable to
determine a better bound in a local region around
, it might be preferable to
determine a better bound in a local region around
![]() . A
linear method could be obtained by analyzing the Jacobian of the
transformations, such as (3.53) and
(3.57).
. A
linear method could be obtained by analyzing the Jacobian of the
transformations, such as (3.53) and
(3.57).
Another important concern when checking a path is the order in which
the samples are checked. For simplicity, suppose that ![]() is
constant and that the path is a constant-speed parameterization.
Should the collision checker step along from 0 up to
is
constant and that the path is a constant-speed parameterization.
Should the collision checker step along from 0 up to ![]() ?
Experimental evidence indicates that it is best to use a recursive
binary strategy [379]. This makes no difference if the path
is collision-free, but it often saves time if the path is in
collision. This is a kind of sampling problem over
?
Experimental evidence indicates that it is best to use a recursive
binary strategy [379]. This makes no difference if the path
is collision-free, but it often saves time if the path is in
collision. This is a kind of sampling problem over ![]() , which is
addressed nicely by the van der Corput sequence,
, which is
addressed nicely by the van der Corput sequence, ![]() . The
last column in Figure 5.2 indicates precisely where to
check along the path in each step. Initially,
. The
last column in Figure 5.2 indicates precisely where to
check along the path in each step. Initially, ![]() is checked.
Following this, points from the van der Corput sequence are
checked in order:
is checked.
Following this, points from the van der Corput sequence are
checked in order: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() . The process terminates if a collision is
found or when the dispersion falls below
. The process terminates if a collision is
found or when the dispersion falls below ![]() . If
. If ![]() is not constant, then it is possible to skip over some points of
is not constant, then it is possible to skip over some points of
![]() in regions where the allowable variation in
in regions where the allowable variation in ![]() is larger.
is larger.
Steven M LaValle 2020-08-14