Suppose a rotation by 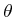 is performed, followed by a translation
by
is performed, followed by a translation
by  . This can be used to place the robot in any desired
position and orientation. Note that translations and rotations do not
commute! If the operations are applied successively, each
. This can be used to place the robot in any desired
position and orientation. Note that translations and rotations do not
commute! If the operations are applied successively, each
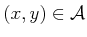 is transformed to
is transformed to
 |
(3.33) |
The following matrix multiplication yields the same result for the
first two vector components:
 |
(3.34) |
This implies that the
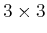 matrix,
matrix,
 |
(3.35) |
represents a rotation followed by a translation. The matrix 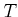 will
be referred to as a homogeneous transformation matrix. It is
important to remember that
will
be referred to as a homogeneous transformation matrix. It is
important to remember that 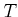 represents a rotation followed by
a translation (not the other way around). Each primitive can be
transformed using the inverse of
represents a rotation followed by
a translation (not the other way around). Each primitive can be
transformed using the inverse of 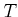 , resulting in a transformed solid
model of the robot. The transformed robot is denoted by
, resulting in a transformed solid
model of the robot. The transformed robot is denoted by
 , and in this case there are three degrees of
freedom. The homogeneous transformation matrix is a convenient
representation of the combined transformations; therefore, it is
frequently used in robotics, mechanics, computer graphics, and
elsewhere. It is called homogeneous because over
, and in this case there are three degrees of
freedom. The homogeneous transformation matrix is a convenient
representation of the combined transformations; therefore, it is
frequently used in robotics, mechanics, computer graphics, and
elsewhere. It is called homogeneous because over
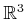 it is just a
linear transformation without any translation. The trick of
increasing the dimension by one to absorb the translational part is
common in projective geometry [804].
it is just a
linear transformation without any translation. The trick of
increasing the dimension by one to absorb the translational part is
common in projective geometry [804].
Steven M LaValle
2020-08-14

![]() is performed, followed by a translation
by
is performed, followed by a translation
by ![]() . This can be used to place the robot in any desired
position and orientation. Note that translations and rotations do not
commute! If the operations are applied successively, each
. This can be used to place the robot in any desired
position and orientation. Note that translations and rotations do not
commute! If the operations are applied successively, each
![]() is transformed to
is transformed to

