The robot, 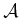 , can be rotated counterclockwise by some angle
, can be rotated counterclockwise by some angle
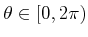 by mapping every
by mapping every
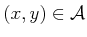 as
as
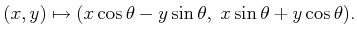 |
(3.30) |
Using a
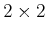 rotation matrix,
rotation matrix,
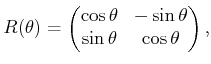 |
(3.31) |
the transformation can be written as
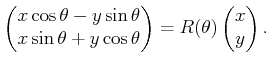 |
(3.32) |
Using the notation of Section 3.2.1,  becomes
becomes  , for which
, for which
 . For linear transformations,
such as the one defined by (3.32), recall that the column
vectors represent the basis vectors of the new coordinate frame. The
column vectors of
. For linear transformations,
such as the one defined by (3.32), recall that the column
vectors represent the basis vectors of the new coordinate frame. The
column vectors of  are unit vectors, and their inner
product (or dot product) is zero, indicating that they are orthogonal.
Suppose that the
are unit vectors, and their inner
product (or dot product) is zero, indicating that they are orthogonal.
Suppose that the 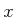 and
and 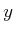 coordinate axes, which represent the body
frame, are ``painted'' on
coordinate axes, which represent the body
frame, are ``painted'' on 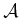 . The columns of
. The columns of  can be
derived by considering the resulting directions of the
can be
derived by considering the resulting directions of the 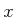 - and
- and
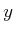 -axes, respectively, after performing a counterclockwise rotation
by the angle
-axes, respectively, after performing a counterclockwise rotation
by the angle 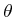 . This interpretation generalizes nicely for
higher dimensional rotation matrices.
. This interpretation generalizes nicely for
higher dimensional rotation matrices.
Note that the rotation is performed about the origin. Thus, when
defining the model of 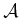 , the origin should be placed at the
intended axis of rotation. Using the semi-algebraic model, the entire
robot model can be rotated by transforming each primitive, yielding
, the origin should be placed at the
intended axis of rotation. Using the semi-algebraic model, the entire
robot model can be rotated by transforming each primitive, yielding
 . The inverse rotation,
. The inverse rotation,
 , must be applied to
each primitive.
, must be applied to
each primitive.
Steven M LaValle
2020-08-14

![]() , can be rotated counterclockwise by some angle
, can be rotated counterclockwise by some angle
![]() by mapping every
by mapping every
![]() as
as
![]() , the origin should be placed at the
intended axis of rotation. Using the semi-algebraic model, the entire
robot model can be rotated by transforming each primitive, yielding
, the origin should be placed at the
intended axis of rotation. Using the semi-algebraic model, the entire
robot model can be rotated by transforming each primitive, yielding
![]() . The inverse rotation,
. The inverse rotation,
![]() , must be applied to
each primitive.
, must be applied to
each primitive.