- Characterize the stability at
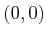 of the vector field on
of the vector field on
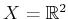 , given by
, given by
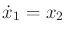 and
and
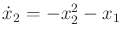 . Use
the Lyapunov function
. Use
the Lyapunov function
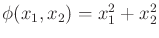 .
.
- Repeat Example 15.4, but instead use the cost term
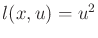 .
.
- Repeat Example 15.4, but instead for a triple
integrator
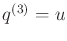 and
and
![$ U = [-1,1]$](img3387.gif) .
.
- Determine the precise conditions under which each of the four
cases of Example 15.4 occurs. Define a feedback motion
plan that causes time-optimal motions.
- Note that some of the six optimal words for the Dubins car do
not appear for the Reeds-Shepp car. For each of these, illustrate why
it does not appear.
- Retrace the steps of the Taylor series argument for deriving the
Lie bracket in Section 15.4.2. Arrive at (15.81) by
showing all steps in detail (smaller steps are skipped in Section
15.4.2).
- Determine whether the following system is nonholonomic and STLC:
- Prove that linear systems
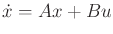 for constant
matrices
for constant
matrices 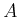 and
and 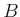 cannot be nonholonomic.
cannot be nonholonomic.
- Determine whether the following system is nonholonomic and STLC:
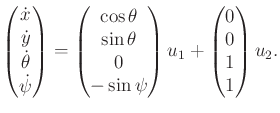 |
(15.167) |
- Using the commutator motion and constant actions for the
differential drive, develop a lattice over its configuration space.
- Consider a smooth nonlinear system that has only one action
variable and an
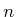 -dimensional state space for
-dimensional state space for 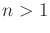 . Are such
systems always completely integrable, always nonholonomic, or is either possible?
. Are such
systems always completely integrable, always nonholonomic, or is either possible?
- Generalize Example 15.17 to
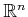 with two action
variables. Determine whether the system is STLC for any
with two action
variables. Determine whether the system is STLC for any 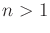 .
.
- Show that the vector cross product on
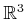 indeed produces
a Lie algebra when used as a bracket operation.
indeed produces
a Lie algebra when used as a bracket operation.
- Derive the CFS equation for the following system:
Implementations
- Implement software that computes the P. Hall basis up to any
desired order (this is only symbolic computation; the Lie
brackets are not expanded).
- Implement software that displays the appropriate optimal path for
the Dubins car, between any given
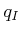 and
and 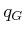 .
.
- Apply the planning algorithm in Section 14.4.2 to
numerically determine the Dubins curves. Use Dijkstra's algorithm for
the search, and use a high-resolution grid. Can your software obtain
the same set of curves as Dubins?
- Experiment with using Dubins curves as a local planning method
(LPM) and metric in an RRT-based planning algorithm. Does using the
curves improve execution time? Do they lead to better solutions?
Steven M LaValle
2020-08-14
