
Next: 15.4.3.3 Philip Hall basis Up: 15.4.3 Determining Controllability Previous: 15.4.3.1 The Lie algebra
Now suppose that a set ![]() ,
, ![]() ,
, ![]() of vector fields is
given as a driftless control-affine system, as in
(15.53). Its associated distribution
of vector fields is
given as a driftless control-affine system, as in
(15.53). Its associated distribution
![]() is
interpreted as a vector space with coefficients in
is
interpreted as a vector space with coefficients in
![]() , and the Lie
bracket operation was given by (15.81). It can be verified
that the Lie bracket operation in (15.81) satisfies the
required axioms for a Lie algebra.
, and the Lie
bracket operation was given by (15.81). It can be verified
that the Lie bracket operation in (15.81) satisfies the
required axioms for a Lie algebra.
As observed in Examples 15.9 and 15.10, the Lie
bracket may produce vector fields outside of
![]() . By defining
the Lie algebra of
. By defining
the Lie algebra of
![]() to be all vector fields that can be
obtained by applying Lie bracket operations, a potentially larger
distribution
to be all vector fields that can be
obtained by applying Lie bracket operations, a potentially larger
distribution
![]() is obtained. The Lie algebra can be
expressed using the
is obtained. The Lie algebra can be
expressed using the
![]() notation by including
notation by including ![]() ,
, ![]() ,
,
![]() and all independent vector fields generated by Lie brackets.
Note that no more than
and all independent vector fields generated by Lie brackets.
Note that no more than ![]() independent vector fields can possibly be
produced.
independent vector fields can possibly be
produced.
| (15.101) |
Let the system be
The first Lie bracket produces
| (15.103) |
| (15.104) |
| (15.105) |
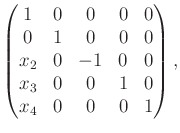 |
(15.106) |
| (15.107) |
![]()
Steven M LaValle 2020-08-14