
Next: Time optimality Up: 15.2 Continuous-Time Dynamic Programming Previous: 15.2.2 Linear-Quadratic Problems
Pontryagin's minimum principle15.5 is closely related to the HJB equation and provides conditions that an optimal trajectory must satisfy. Keep in mind, however, that the minimum principle provides necessary conditions, but not sufficient conditions, for optimality. In contrast, the HJB equation offered sufficient conditions. Using the minimum principle alone, one is often not able to conclude that a trajectory is optimal. In some cases, however, it is quite useful for finding candidate optimal trajectories. Any trajectory that fails to satisfy the minimum principle cannot be optimal.
To understand the minimum principle, we first return to the case of
discrete planning. As mentioned previously, the minimum principle is
essentially given by (15.7). This can be considered as a
specialization of the HJB equation to the special case of applying the
optimal action ![]() . This causes the
. This causes the ![]() to disappear, but along
with it the global properties of the HJB equation also vanish. The
minimum principle expresses conditions along the optimal trajectory,
as opposed to the cost-to-go function over the whole state space.
Therefore, it can at best assure local optimality in the space of
possible trajectories.
to disappear, but along
with it the global properties of the HJB equation also vanish. The
minimum principle expresses conditions along the optimal trajectory,
as opposed to the cost-to-go function over the whole state space.
Therefore, it can at best assure local optimality in the space of
possible trajectories.
The minimum principle for the continuous case is essentially given by (15.15), which is the continuous-time counterpart to (15.7). However, it is usually expressed in terms of adjoint variables and a Hamiltonian function, in the spirit of Hamiltonian mechanics from Section 13.4.4.
Let ![]() denote an
denote an ![]() -dimensional vector of adjoint
variables, which are defined as
-dimensional vector of adjoint
variables, which are defined as
Under the execution of the optimal action trajectory
![]() , the
HJB equation implies that
, the
HJB equation implies that
Using the HJB equation (15.14), the optimal action is given by
The missing piece of information so far is how ![]() evolves over
time. It turns out that a system of the form
evolves over
time. It turns out that a system of the form
Remember that ![]() is defined in (15.25) just to keep
track of the change in
is defined in (15.25) just to keep
track of the change in ![]() . It would be helpful to have an
explicit form for (15.29). Suppose that
. It would be helpful to have an
explicit form for (15.29). Suppose that ![]() is
selected by a feedback plan to yield
is
selected by a feedback plan to yield
![]() . In this
case, the Hamiltonian can be interpreted as a function of only
. In this
case, the Hamiltonian can be interpreted as a function of only ![]() and
and
![]() . Under this assumption, differentiating the Hamiltonian
(15.26) with respect to
. Under this assumption, differentiating the Hamiltonian
(15.26) with respect to ![]() yields
yields
The second term in (15.30) is actually
![]() ,
although it is hard to see at first. The total differential of
,
although it is hard to see at first. The total differential of
![]() with respect to the state is
with respect to the state is
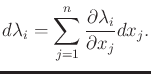 |
(15.31) |
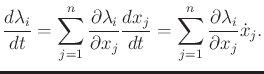 |
(15.32) |
The transition equations given by
![]() and
(15.36) specify the evolution of the system given by
the minimum principle. These are analogous to Hamilton's equations
(13.198), which were given in Section 13.4.4.
The generalized momentum in that context becomes the adjoint variables
here.
and
(15.36) specify the evolution of the system given by
the minimum principle. These are analogous to Hamilton's equations
(13.198), which were given in Section 13.4.4.
The generalized momentum in that context becomes the adjoint variables
here.
When applying the minimum principle, it is usually required to use the fact that the optimal action at all times must satisfy (15.28). Often, this is equivalently expressed as
Using (15.26), the Hamiltonian is defined as
The only remaining task is to determine the values of the adjoint
variables over time. The adjoint transition equation is obtained from
(15.36) as
![]() and
and
![]() . The solutions are
. The solutions are
![]() and
and
![]() , in which
, in which ![]() and
and ![]() are constants that can be
determined at
are constants that can be
determined at ![]() from (15.38) and
(15.39). The optimal action depends only on the sign of
from (15.38) and
(15.39). The optimal action depends only on the sign of
![]() . Since its solution is the equation of a line, it
can change signs at most once. Therefore, there are four possible
kinds of solutions, depending on the particular
. Since its solution is the equation of a line, it
can change signs at most once. Therefore, there are four possible
kinds of solutions, depending on the particular ![]() and
and ![]() :
:
This was one of the simplest possible examples, and the optimal solution was easily found because the adjoint variables are linear functions of time. Section 15.3 covers optimal solutions for the Dubins car, the Reeds-Shepp car, and the differential drive, all of which can be established using the minimum principle combined with some geometric arguments. As systems become more complicated, such analysis is unfortunately too difficult. In these cases, sampling-based methods, such as those of Chapter 14, must be used to determine optimal trajectories.
One common complication is the existence of singular arcs along
the solution trajectory. These correspond to a degeneracy in ![]() with
respect to
with
respect to ![]() over some duration of time. This could be caused, for
example, by having
over some duration of time. This could be caused, for
example, by having ![]() independent of
independent of ![]() . In Example
15.4,
. In Example
15.4, ![]() became independent of
became independent of ![]() when
when
![]() ; however, there was no singular arc because this could only occur
for an instant of time. If the duration had been longer, then there
would be an interval of time over which the optimal action could not
be determined. In general, if the Hessian (recall definition from
(8.48)) of
; however, there was no singular arc because this could only occur
for an instant of time. If the duration had been longer, then there
would be an interval of time over which the optimal action could not
be determined. In general, if the Hessian (recall definition from
(8.48)) of ![]() with respect to
with respect to ![]() is a positive definite
matrix, then there are no singular arcs (this is often called the
Legendre-Clebsch condition). The minimum principle in this case
provides a sufficient condition for local optimality in the space of
possible state trajectories. If the Hessian is not positive definite
for some interval
is a positive definite
matrix, then there are no singular arcs (this is often called the
Legendre-Clebsch condition). The minimum principle in this case
provides a sufficient condition for local optimality in the space of
possible state trajectories. If the Hessian is not positive definite
for some interval ![]() with
with ![]() , then additional
information is needed to determine the optimal trajectory over the
singular arc from
, then additional
information is needed to determine the optimal trajectory over the
singular arc from ![]() to
to ![]() .
.
Note that all of this analysis ignores the existence of obstacles.
There is nothing to prevent the solutions from attempting to enter an
obstacle region. The action set ![]() and cost
and cost ![]() can be
adjusted to account for obstacles; however, determining an optimal
solution from the minimum principle becomes virtually impossible,
except in some special cases.
can be
adjusted to account for obstacles; however, determining an optimal
solution from the minimum principle becomes virtually impossible,
except in some special cases.
There are other ways to derive the minimum principle. Recall from
Section 13.4.4 that Hamilton's equations can be
derived from the Euler-Lagrange equation. It should not be
surprising that the minimum principle can also be derived using
variational principles [95,789]. The minimum principle can
also be interpreted as a form of constrained optimization. This
yields the interpretation of ![]() as Lagrange multipliers. A
very illuminating reference for further study of the minimum principle
is Pontryagin's original works [801].
as Lagrange multipliers. A
very illuminating reference for further study of the minimum principle
is Pontryagin's original works [801].