
Next: 13.5 Multiple Decision Makers Up: 13.4 Advanced Mechanics Concepts Previous: 13.4.3.2 Nonconservative forces
The Lagrangian formulation of mechanics is the most convenient for
determining a state transition equation for a collection of bodies.
Once the kinetic and potential energies are determined, the remaining
efforts are straightforward computation of derivatives and algebraic
manipulation. Hamiltonian mechanics provides an alternative
formulation that is closely related to the Lagrangian. Instead of
expressing second-order differential constraints on an ![]() -dimensional
C-space, it expresses first-order constraints on a
-dimensional
C-space, it expresses first-order constraints on a ![]() -dimensional
phase space. This idea should be familiar from Section
13.2. The new phase space considered here is an example of
a symplectic manifold, which has many important properties, such
as being orientable and having an even number of dimensions
[39]. The standard phase vector is defined as
-dimensional
phase space. This idea should be familiar from Section
13.2. The new phase space considered here is an example of
a symplectic manifold, which has many important properties, such
as being orientable and having an even number of dimensions
[39]. The standard phase vector is defined as
![]() ; however, instead of
; however, instead of ![]() ,
, ![]() variables will be
introduced and denoted as
variables will be
introduced and denoted as ![]() . Thus, a transformation exists between
. Thus, a transformation exists between
![]() and
and ![]() . The
. The ![]() variables are related to the
configuration variables through a special function over the phase
space called the Hamiltonian.
Although the Hamiltonian formulation usually does not help in the
determination of
variables are related to the
configuration variables through a special function over the phase
space called the Hamiltonian.
Although the Hamiltonian formulation usually does not help in the
determination of
![]() , it is covered here because its
generalization to optimal control problems is quite powerful. This
generalization is called Pontryagin's minimum principle and is
covered in Section 15.2.3. In the context of mechanics, it
provides a general expression of energy conservation laws, which aids
in proving many theoretical results [39,397].
, it is covered here because its
generalization to optimal control problems is quite powerful. This
generalization is called Pontryagin's minimum principle and is
covered in Section 15.2.3. In the context of mechanics, it
provides a general expression of energy conservation laws, which aids
in proving many theoretical results [39,397].
The relationship between
![]() and
and ![]() can be obtained by
using the Legendre transformation [39,397]. Consider
a real-valued function
can be obtained by
using the Legendre transformation [39,397]. Consider
a real-valued function ![]() of two variables,
of two variables,
![]() . Its
total differential [508] is
. Its
total differential [508] is
| (13.188) |
| (13.189) |
Assume that the dynamics do not depend on the particular time (the
extension to time-varying dynamics is not difficult; see
[39,397]). Let
![]() be the Lagrangian
function defined (13.129). Let
be the Lagrangian
function defined (13.129). Let
![]() represent a
generalized momentum vector (or adjoint variables), which
serves the same purpose as
represent a
generalized momentum vector (or adjoint variables), which
serves the same purpose as ![]() in (13.185). Each
in (13.185). Each ![]() is
defined as
is
defined as
Considered as a function of ![]() and
and ![]() only, the total
differential of
only, the total
differential of ![]() is
is
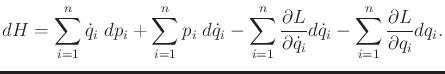 |
(13.194) |
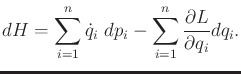 |
(13.195) |
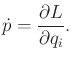 |
(13.196) |
Hamilton's equations are equivalent to the Euler-Lagrange equation.
Extremals in both cases yield equivalent differential constraints.
The difference is that the Lagrangian formulation uses
![]() and the Hamiltonian uses
and the Hamiltonian uses ![]() . The Hamiltonian results in
first-order partial differential equations. It was assumed here that
the dynamics are time-invariant and the motions occur in a
conservative field. In this case,
. The Hamiltonian results in
first-order partial differential equations. It was assumed here that
the dynamics are time-invariant and the motions occur in a
conservative field. In this case, ![]() , which corresponds to
conservation of total energy. In the time-varying case, the
additional equation
, which corresponds to
conservation of total energy. In the time-varying case, the
additional equation
![]() appears along with Hamilton's equations. As stated previously,
Hamilton's equations are primarily of interest in establishing basic
results in theoretical mechanics, as opposed to determining the
motions of particular systems. For example, the Hamiltonian is used
to establish Louisville's theorem, which states that phase flows
preserve volume, implying that a Hamiltonian system cannot be
asymptotically stable [39]. Asymptotic stability is covered
in Section 15.1.1. Pontryagin's minimum principle,
an extension of Hamilton's equations to optimal control theory, is
covered in 15.2.3.
appears along with Hamilton's equations. As stated previously,
Hamilton's equations are primarily of interest in establishing basic
results in theoretical mechanics, as opposed to determining the
motions of particular systems. For example, the Hamiltonian is used
to establish Louisville's theorem, which states that phase flows
preserve volume, implying that a Hamiltonian system cannot be
asymptotically stable [39]. Asymptotic stability is covered
in Section 15.1.1. Pontryagin's minimum principle,
an extension of Hamilton's equations to optimal control theory, is
covered in 15.2.3.
Steven M LaValle 2020-08-14