
Next: 13.4.1.3 Applying actions Up: 13.4.1 Lagrangian Mechanics Previous: 13.4.1.1 Calculus of variations
Now sufficient background has been given to return to the dynamics of
mechanical systems. The path through the C-space of a system of
bodies can be expressed as the solution to a calculus of variations
problem that optimizes the difference between kinetic and potential
energy. The calculus of variations principles
generalize to any coordinate neighborhood of ![]() . In this case, the
Euler-Lagrange equation is
. In this case, the
Euler-Lagrange equation is
The coming presentation will use (13.124) to obtain
a phase transition equation. This will be derived by optimizing a
functional defined as the change in kinetic and potential energy.
Kinetic energy for particles and rigid bodies
was defined in Section 13.3.1. In general, the kinetic
energy function must be a quadratic function of ![]() . Its
definition can be interpreted as an inner product on
. Its
definition can be interpreted as an inner product on ![]() , which
causes
, which
causes ![]() to become a Riemannian manifold [156].
This gives the manifold a notion of the ``angle'' between velocity
vectors and leads to well-defined notions of curvature and shortest
paths called geodesics. Let
to become a Riemannian manifold [156].
This gives the manifold a notion of the ``angle'' between velocity
vectors and leads to well-defined notions of curvature and shortest
paths called geodesics. Let
![]() denote the
kinetic energy, expressed using the manifold coordinates, which
always takes the form
denote the
kinetic energy, expressed using the manifold coordinates, which
always takes the form
The next step is to define potential energy. A system is called conservative if the forces acting on a point
depend only on the point's location, and the work done by the
force along a path depends only on the endpoints of the path.
The total energy is conserved under the motion of a conservative
system. In this case, there exists a potential function
![]() such that
such that
![]() , for
any
, for
any ![]() . Let
. Let ![]() denote the total potential energy of
a collection of bodies, placed at configuration
denote the total potential energy of
a collection of bodies, placed at configuration ![]() .
.
It will be assumed that the dynamics are time-invariant.
Hamilton's principle of least action states that the trajectory,
![]() , of a mechanical system coincides with
extremals of the functional,
, of a mechanical system coincides with
extremals of the functional,
The advantage of the Lagrangian formulation is that the C-space does
not have to be
![]() , described in an inertial
frame. The Euler-Lagrange
equation gives a necessary condition for the motions in any C-space
of a mechanical system. The conditions can be expressed in terms of
any coordinate neighborhood, as opposed to orthogonal coordinate
systems, which are required by the Newton-Euler formulation. In
mechanics literature, the
, described in an inertial
frame. The Euler-Lagrange
equation gives a necessary condition for the motions in any C-space
of a mechanical system. The conditions can be expressed in terms of
any coordinate neighborhood, as opposed to orthogonal coordinate
systems, which are required by the Newton-Euler formulation. In
mechanics literature, the ![]() variables are often referred to as
generalized coordinates. This simply means the coordinates
given by any coordinate neighborhood of a smooth manifold.
variables are often referred to as
generalized coordinates. This simply means the coordinates
given by any coordinate neighborhood of a smooth manifold.
Thus, the special form of (13.124) that uses (13.129) yields the appropriate constraints on the motion:
| (13.132) |
To obtain the differential constraints on the motion of the particle,
use (13.130). For each ![]() from
from ![]() to
to ![]() ,
,
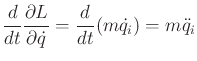 |
(13.133) |
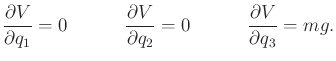 |
(13.134) |
| (13.135) |
The ``least'' part of Hamilton's principle is actually a misnomer. It is technically only a principle of ``extremal'' action because (13.130) can also yield motions that maximize the functional.
Steven M LaValle 2020-08-14