15.3.3 Balkcom-Mason Curves

In recent years, two more families of optimal curves have been determined [64,211]. Recall the differential-drive system from Section 13.1.2, which appears in many mobile robot systems. In many ways, it appears that the differential drive is a special case of the simple car. The expression of the system given in (13.17) can be made to appear identical to the Reeds-Shepp car system in (15.48). For example, letting $r = 1$ and $L = 1$ makes them equivalent by assigning $u_\omega = u_1$ and $u_\psi = u_1 u_2$. Consider the distance traveled by a point attached to the center of the differential-drive axle using (15.42). Minimizing this distance for any ${q_{I}}$ and ${q_{G}}$ is trivial, as shown in Figure 13.4 of Section 13.1.2. The center point can be made to travel in a straight line in ${\cal W}= {\mathbb{R}}^2$. This would be possible for the Reeds-Shepp car if $\rho_{min} = 0$, which implies that $\phi_{max} = \pi/2$. It therefore appeared for many years that no interesting curves exist for the differential drive.

The problem, however, with measuring the distance traveled by the axle center is that pure rotations are cost-free. This occurs when the wheels rotate at the same speed but with opposite angular velocities. The center does not move; however, the time duration, energy expenditure, and wheel rotations that occur are neglected. By incorporating one or more of these into the cost functional, a challenging optimization arises. Balkcom and Mason bounded the speed of the differential drive and minimized the total time that it takes to travel from ${q_{I}}$ to ${q_{G}}$. Using (13.16), the action set is defined as $U = [-1,1] \times [-1,1]$, in which the maximum rotation rate of each wheel is one (an alternative bound can be used without loss of generality). The criterion to optimize is

$$L({\tilde q},{\tilde{u}}) = \int_0^{t_F} \sqrt{{\dot x}(t)^2 + {\dot y}(t)^2} + \vert{\dot \theta}(t)\vert dt ,$$ (15.50)

which takes $\theta$ into account, whereas it was neglected in (15.42). This criterion is once again equivalent to minimizing the time to reach ${q_{G}}$. The resulting model will be referred to as the Balkcom-Mason drive. An alternative criterion is the total amount of wheel rotation; this leads to an alternative family of optimal curves [211].

Figure 15.11: The four motion primitives from which all optimal curves for the differential-drive robot can be constructed.

It was shown in [64] that only the four motion primitives shown in Figure 15.11 are needed to express time-optimal paths for the differential-drive robot. Each primitive corresponds to holding one action variable fixed at its limit for an interval of time. Using the symbols in Figure 15.11 (which were used in [64]), words can be formed that describe the optimal path. It has been shown that the word length is no more than five. Thus, any shortest paths may be expressed as a piecewise-constant action trajectory in which there are no more than five pieces. Every piece corresponds to one of the primitives in Figure 15.11.

Figure 15.12: Each of the nine base words is depicted [64]. The last two are only valid for small motions; they are magnified five times and the robot outline is not drawn.

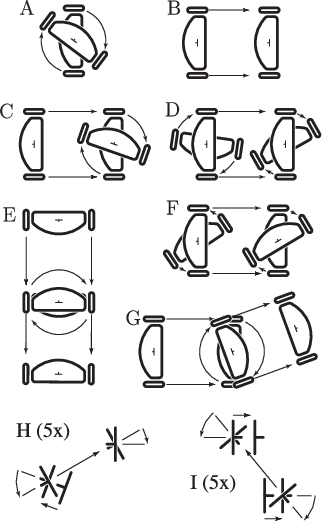It is convenient in the case of the Balkcom-Mason drive to use the same symbols for both base words and for precise specification of primitives. Symmetry transformations will be applied to each base word to yield a family of eight words that precisely specify the sequences of motion primitives. Nine base words describe the shortest paths:

$$\begin{split}\{ \ensuremath{\curvearrowright}, \;\; \ensurema... ...suremath{\curvearrowright}\ensuremath{\Uparrow}\} . \end{split}$$ (15.51)

This is analogous to the compressed forms given in (15.46) and (15.49). The motions are depicted in Figure 15.12.

Figure 15.13: The 40 optimal curve types for the differential-drive robot, sorted by symmetry class [64].

Figure 15.13 shows 40 distinct Balkcom-Mason curves that result from applying symmetry transformations to the base words of (15.51). There are 72 entries in Figure 15.13, but many are identical. The transformation $T_1$ indicates that the directions of $\ensuremath{\Uparrow}$ and $\ensuremath{\Downarrow}$ are flipped from the base word. The transformation $T_2$ reverses the order of the motion primitives. The transformation $T_3$ flips the directions of $\ensuremath{\curvearrowleft}$ and $\ensuremath{\curvearrowright}$. The transformations commute, and there are seven possible ways to combine them, which contributes to a row of Figure 15.13.

Figure 15.14: A slice of the optimal curves is shown for ${q_{I}}= (x, y, \frac {\pi }{4})$ and ${q_{G}}= (0,0,0)$ [64]. Level sets of the optimal cost-to-go $G^*$ are displayed. The coordinates correspond to a differential drive with $r = L = 1$ in (13.16).

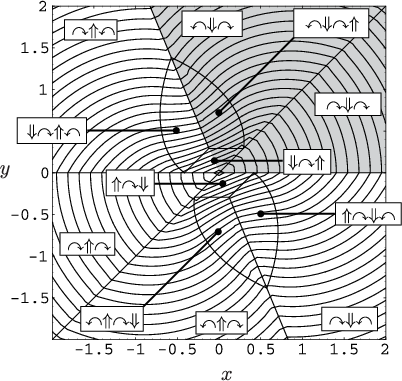To construct an LPM or distance function, the same issues arise as for the Reeds-Shepp and Dubins cars. Rather than testing all $40$ words to find the shortest path, simple tests can be defined over which a particular word becomes active [64]. A slice of the precise cell decomposition and the resulting optimal cost-to-go (which can be called the Balkcom-Mason metric) are shown in Figure 15.14.