
Next: 15.3.2 Reeds-Shepp Curves Up: 15.3 Optimal Paths for Previous: 15.3 Optimal Paths for
Recall the Dubins version of the simple car given in Section
13.1.2. The system was specified in (13.15).
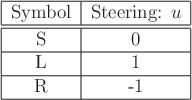
It is assumed here that the car moves at constant forward speed, ![]() . The other important constraint is the maximum steering angle
. The other important constraint is the maximum steering angle
![]() , which results in a minimum turning radius
, which results in a minimum turning radius
![]() .
As the car travels, consider the length of the curve in
.
As the car travels, consider the length of the curve in
![]() traced out by a pencil attached to the center of the rear axle. This
is the location of the body-frame origin in Figure 13.1.
The task is to minimize the length of this curve as the car travels
between any
traced out by a pencil attached to the center of the rear axle. This
is the location of the body-frame origin in Figure 13.1.
The task is to minimize the length of this curve as the car travels
between any ![]() and
and ![]() . Due to
. Due to
![]() , this can be
considered as a bounded-curvature shortest-path problem. If
, this can be
considered as a bounded-curvature shortest-path problem. If
![]() , then there is no curvature bound, and the shortest
path follows a straight line in
, then there is no curvature bound, and the shortest
path follows a straight line in
![]() . In terms of a
cost functional of the form (8.39), the criterion to
optimize is
. In terms of a
cost functional of the form (8.39), the criterion to
optimize is
Since the speed is constant, the system can be simplified to
 |
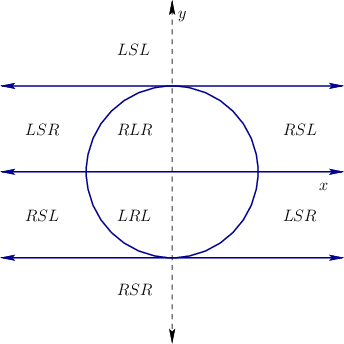
It was shown in [294] that between any two configurations, the
shortest path for the Dubins car can always be expressed as a
combination of no more than three motion primitives. Each motion
primitive applies a constant action over an interval of time.
Furthermore, the only actions that are needed to traverse the shortest
paths are
![]() . The primitives and their associated
symbols are shown in Figure 15.3. The
. The primitives and their associated
symbols are shown in Figure 15.3. The ![]() primitive
drives the car straight ahead. The
primitive
drives the car straight ahead. The ![]() and
and ![]() primitives turn as
sharply as possible to the left and right, respectively. Using these
symbols, each possible kind of shortest path can be designated as a
sequence of three symbols that corresponds to the order in which the
primitives are applied. Let such a sequence be called a word
. There is no need to
have two consecutive primitives of the same kind because they can be
merged into one. Under this observation, ten possible words of length
three are possible. Dubins showed that only these six words are
possibly optimal:
primitives turn as
sharply as possible to the left and right, respectively. Using these
symbols, each possible kind of shortest path can be designated as a
sequence of three symbols that corresponds to the order in which the
primitives are applied. Let such a sequence be called a word
. There is no need to
have two consecutive primitives of the same kind because they can be
merged into one. Under this observation, ten possible words of length
three are possible. Dubins showed that only these six words are
possibly optimal:
To be more precise, the duration of each primitive should also be
specified. For ![]() or
or ![]() , let a subscript denote the total amount of
rotation that accumulates during the application of the primitive.
For
, let a subscript denote the total amount of
rotation that accumulates during the application of the primitive.
For ![]() , let a subscript denote the total distance traveled. Using
such subscripts, the Dubins curves can be more precisely characterized
as
, let a subscript denote the total distance traveled. Using
such subscripts, the Dubins curves can be more precisely characterized
as
It will be convenient to invent a compressed form of the words to
group together paths that are qualitatively similar. This will be
particularly valuable when Reeds-Shepp curves are introduced in
Section 15.3.2 because there are 46 of them, as opposed to
![]() Dubins curves. Let
Dubins curves. Let ![]() denote a symbol that means ``curve,'' and
represents either
denote a symbol that means ``curve,'' and
represents either ![]() or
or ![]() . Using
. Using ![]() , the six words in
(15.44) can be compressed to only two base words:
, the six words in
(15.44) can be compressed to only two base words:
 |
Powerful information has been provided so far for characterizing the
shortest paths; however, for a given ![]() and
and ![]() , two
problems remain:
, two
problems remain:
 |
In addition to use as an LPM, the
resulting cost of the shortest path may be a useful distance function
in many sampling-based planning algorithms. This is sometimes called
the Dubins metric (it is not, however, a true metric because it
violates the symmetry axiom). This can be considered as the optimal
cost-to-go ![]() . It could have been computed approximately using
the dynamic programming approach in Section 14.5; however,
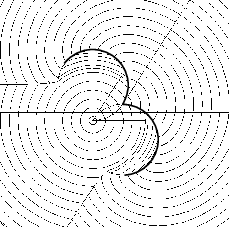
thanks to careful analysis, the exact values are known. One
interesting property of the Dubins metric is that it is discontinuous;
see Figure 15.6. Compare the cost of traveling
. It could have been computed approximately using
the dynamic programming approach in Section 14.5; however,
thanks to careful analysis, the exact values are known. One
interesting property of the Dubins metric is that it is discontinuous;
see Figure 15.6. Compare the cost of traveling ![]() using the
using the ![]() primitive to the cost of traveling to a nearby point
that would require a smaller turning radius than that achieved by the
primitive to the cost of traveling to a nearby point
that would require a smaller turning radius than that achieved by the
![]() primitive. The required action does not exist in
primitive. The required action does not exist in ![]() , and the
point will have to be reached by a longer sequence of primitives. The
discontinuity in
, and the
point will have to be reached by a longer sequence of primitives. The
discontinuity in ![]() is enabled by the fact that the Dubins car
fails to possess the STLC
property from Section 15.1.3. For STLC systems,
is enabled by the fact that the Dubins car
fails to possess the STLC
property from Section 15.1.3. For STLC systems,
![]() is continuous.
is continuous.
Steven M LaValle 2020-08-14