15.3.2 Reeds-Shepp Curves

Now consider the shortest paths of the Reeds-Shepp car. The only difference in comparison to the Dubins car is that travel in the reverse direction is now allowed. The same criterion (15.42) is optimized, which is the distance traveled by the center of the rear axle. The shortest path is equivalent to the path that takes minimum time, as for the Dubins car. The simplified system in (15.43) can be enhanced to obtain

$$\begin{split}{\dot x}& = u_1 \cos \theta \\ {\dot y}& = u_1 \sin \theta \\ {\dot \theta}& = u_1 u_2 , \end{split}$$ (15.48)

in which $u_1 \in \{-1,1\}$ and $u_2 \in [-\tan \phi_{max},\tan \phi_{max}]$. The first action variable, $u_1$, selects the gear, which is forward ($u_1 = 1$) or reverse ($u_1 = -1$). Once again, assume for simplicity that $u_2 \in [-1,1]$. The results stated here apply to any $\phi_{max} \in (0,\pi/2)$.

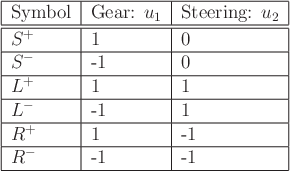
It was shown in [814] that there are no more than 48 different words that describe the shortest paths for the Reeds-Shepp car. The base word notation from Section 15.3.1 can be extended to nicely express the shortest paths. A new symbol, ``$\,\vert\,$'', is used in the words to indicate that the ``gear'' is shifted from forward to reverse or reverse to forward. Reeds and Shepp showed that the shortest path for their car can always be expressed with one of the following base words:

$$\begin{split}\{ & C\vert C\vert C, \;\; CC\vert C, \;\; C\ver... ...vert C, \;\; C\vert C_{\pi/2}SC_{\pi/2}\vert C \} . \end{split}$$ (15.49)

As many as five primitives could be needed to execute the shortest path. A subscript of $\pi/2$ is given in some cases because the curve must be followed for precisely $\pi/2$ radians. For some others, $\beta$ is given as a subscript to indicate that it must match the parameter of another primitive. The form given in (15.49) is analogous to (15.46) for the Dubins car. The parameter ranges can also be specified, to yield a form analogous to (15.47). The result is shown in Figure 15.7. Example curves for two cases are shown in Figure 15.9.

Figure 15.7: The interval ranges are shown for each motion primitive parameter for the Reeds-Shepp optimal curves.

Figure 15.8: The six motion primitives from which all optimal curves for the Reeds-Shepp car can be constructed.

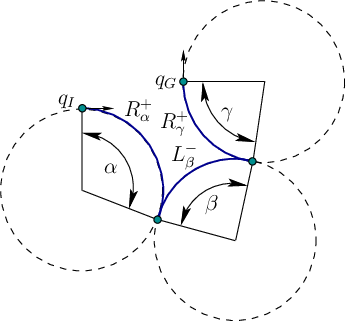
Now the base words will be made more precise by specifying the particular motion primitive. Imagine constructing a list of words analogous to (15.44) for the Dubins car. There are six primitives as shown in Figure 15.8. The symbols $S$, $L$, and $R$ are used again. To indicate the forward or reverse gear, $+$ and $-$ superscripts will be used as shown in Figure 15.8.^15.6

Figure 15.10 shows 48 different words, which result from uncompressing the base words expressed using $C$, $S$, and ``$\,\vert\,$'' in (15.49). Each shortest path is a word with length at most five. There are substantially more words than for the Dubins car. Each base word in (15.49) expands into four or eight words using the motion primitives. To uncompress each base word, the rule that $R$ and $L$ cannot be applied consecutively is maintained. This yields four possibilities for the first six compressed words. The remaining three involve an intermediate $S$ primitive, which allows eight possible sequences of $R$s and $L$s for each one. Two of the 48 words were eliminated in [923]. Each of the remaining 46 words can actually occur for a shortest path and are called the Reeds-Shepp curves.

Figure 15.9: An example of the $R^+_\alpha L^-_\beta R^+_\gamma$ curve. This uses reverse to generate a curve that is shorter than the one in Figure 15.4b for the Dubins car.

Figure 15.10: The 48 curves of Reeds and Shepp. Sussmann and Tang [923] showed that $(L^- R^+ L^-)$ and $(R^- L^+ R^-)$, which appear in the first row, can be eliminated. Hence, only 46 words are needed to describe the shortest paths.

For use as an LPM, the problem appears once again of determining the particular word and parameters for a given ${q_{I}}$ and ${q_{G}}$. This was not difficult for Dubins curves, but now there are 46 possibilities. The naive approach of testing every word and choosing the shortest one may be too costly. The precise cell boundaries in ${\cal C}$ over which each word applies are given in [903]. The cell boundaries are unfortunately quite complicated, which makes the point location algorithm difficult to implement. A simple way to prune away many words from consideration is to use intervals of validity for $\theta$. For some values of $\theta$, certain compressed words are impossible as shortest paths. A convenient table of words that become active over ranges of $\theta$ is given in [903]. Once again, the length of the shortest path can serve as a distance function in sampling-based planning algorithms. The resulting Reeds-Shepp metric is continuous because the Reeds-Shepp car is STLC, which will be established in Section 15.4.