- Characterize
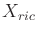 for the case of a point mass in
for the case of a point mass in
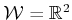 , with each coordinate modeled as a double integrator. Assume
that
, with each coordinate modeled as a double integrator. Assume
that 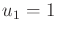 and
and 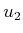 may take any value in
may take any value in ![$ [-1,1]$](img1822.gif) . Determine
. Determine
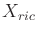 for:
for:
- A point obstacle at
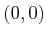 in
in 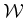 .
.
- A segment from
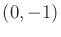 to
to 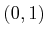 in
in 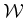 .
.
Characterize the solutions in terms of the phase variables 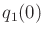 ,
,
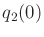 ,
,
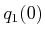 , and
, and
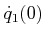 .
.
- Extending the double integrator:
- Develop a lattice for the triple integrator
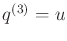 that
extends naturally from the double-integrator lattice.
that
extends naturally from the double-integrator lattice.
- Describe how to develop a lattice for higher order integrators
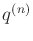 for
for 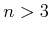 .
.
- Make a figure similar to Figure 14.6b, but for
three stages of the Reeds-Shepp car.
- Determine expressions for the upper and lower boundaries of the
time-limited reachable sets shown in Figure 14.14.
Express them as parabolas, with
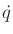 as a function of
as a function of 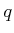 .
.
- A reachability graph can be made by ``rolling'' a polyhedron in
the plane. For example, suppose a solid, regular tetrahedron is
placed on a planar surface. Assuming high friction, the tetrahedron
can be flipped in one of four directions by pushing on the top.
Construct the three-stage reachability graph for this problem.
- Construct a four-stage reachability graph similar to the one
shown in Figure 14.6b, but for the case of a
differential drive robot modeled by (13.17). Use the
three actions
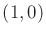 ,
, 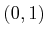 , and
, and 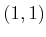 . Draw the graph in the
plane and indicate the configuration coordinates of each vertex.
. Draw the graph in the
plane and indicate the configuration coordinates of each vertex.
- Section 14.2.2 explained how resolution-complete
algorithms exist for planning under differential constraints. Suppose
that in addition to continuous state variables, there are discrete
modes, as introduced in Section 7.3, to form a hybrid
system. Explain how resolution-complete planning algorithms can be
developed for this case. Extend the argument shown in Figure
14.7.
Implementations
- Compare the performance and accuracy of Euler integration to
fourth-order Runge-Kutta on trajectories generated for a single,
double, and triple integrator. For accuracy, compare the results to
solutions obtained analytically. Provide recommendations of which one
to use under various conditions.
- Improve Figure 14.13 by making a plot of the actual
trajectories, which are parabolic in most cases.
- In Figure 14.13, the state trajectory segments are
longer as
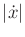 increases. Develop a lattice that tries to keep
all segments as close to the same length as possible by reducing
increases. Develop a lattice that tries to keep
all segments as close to the same length as possible by reducing
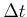 as
as
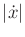 increases. Implement and experiment with
different schemes and report on the results.
increases. Implement and experiment with
different schemes and report on the results.
- Develop an implementation for computing approximately
time-optimal state trajectories for a point mass in a 2D polygonal
world. The robot dynamics can be modeled as two independent double
integrators. Search the double-integrator lattice in
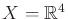 to
solve the problem. Animate the computed solutions.
to
solve the problem. Animate the computed solutions.
- Experiment with RDT methods applied to a spacecraft that is
modeled as a 3D rigid body with thrusters. Develop software that
computes collision-free trajectories for the robot. Carefully study
the issues associated with choosing the metric on
 .
.
- Solve the problem of optimally bringing the Dubins car to a goal
region in a polygonal world by using value iteration with
interpolation.
- Select and implement a planning algorithm that computes pushing
trajectories for a differential drive robot that pushes a box in a
polygonal environment. This was given as an example of a nonholonomic
system in Section 13.1.3. To use the appropriate
constraints on
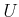 , see [671].
, see [671].
- Select and implement a planning algorithm that computes
trajectories for parking a car while pulling a single trailer,
using (13.19). Make an obstacle region in
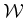 that
corresponds to a tight parking space and vary the amount of
clearance. Also, experiment with driving the vehicle through an
obstacle course.
that
corresponds to a tight parking space and vary the amount of
clearance. Also, experiment with driving the vehicle through an
obstacle course.
- Generate a 3D rendering of reachability graphs for the airplane
model in (13.20). Assume that in each stage there are nine
possible actions, based on combinations of flying to the right, left,
or straight and decreasing, increasing, or maintaining altitude.
- Implement the dynamic programming algorithm shown in Figure
14.27 for the two-link manipulator model given in Example
13.13.
- Implement the bang-bang algorithm shown in Figure
14.28 for the two-link manipulator model given in Example
13.13.
- For the Dubins car (or another system), experiment with
generating a search graph based on Figure 14.7 by
alternating between various step sizes. Plot in the plane, the
vertices and state trajectories associated with the edges of the
graph. Experiment with different schemes for generating a
resolution-complete search graph in a rectangular region and compare
the results.
- Use value iteration with interpolation to compute the optimal
cost-to-go for the Reeds-Shepp car. Plot level sets of the
cost-to-go, which indicate the time-limited reachable sets. Compare
the result to Figure 14.4.
Steven M LaValle
2020-08-14
