14.1.3 Obstacles in the Phase Space

In Formulation 14.1, the specification of the obstacle region in Item 4 was intentionally left ambiguous. Now it will be specified in more detail. If $X = {\cal C}$, then ${X_{obs}}= {\cal C}_{obs}$, which was defined in (4.34) for a rigid robot and in (4.36) for a robot with multiple links. The more interesting case occurs if $X$ is a phase space that includes velocity variables in addition to configuration information.

Figure 14.1: An obstacle region ${\cal C}_{obs}\subset {\cal C}$ generates a cylindrical obstacle region ${X_{obs}}\subset X$ with respect to the phase variables.

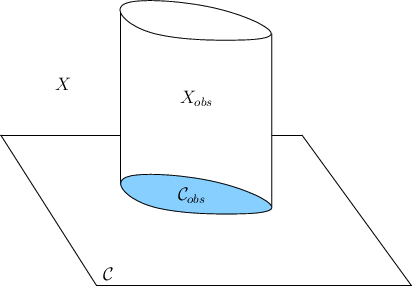Any state for which its associated configuration lies in ${\cal C}_{obs}$ must also be a member of ${X_{obs}}$. The velocity is irrelevant if a collision occurs in the world ${\cal W}$. In most cases that involve a phase space, the obstacle region ${X_{obs}}$ is therefore defined as

$${X_{obs}}= \{ x\in X \;\vert\; {\kappa}(x) \in {\cal C}_{obs}\},$$ (14.2)

in which ${\kappa}(x)$ is the configuration associated with the state $x \in X$. If the first $n$ variables of $X$ are configuration parameters, then ${X_{obs}}$ has the cylindrical structure shown in Figure 14.1 with respect to the other variables. If ${\kappa }$ is a complicated mapping, as opposed to simply selecting the configuration coordinates, then the structure might not appear cylindrical. In these cases, (14.2) still indicates the correct obstacle region in $X$.