- Let
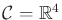 . There are two Pfaffian constraints,
. There are two Pfaffian constraints,
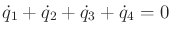 and
and
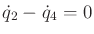 .
Determine the appropriate number of action variables and express the
differential constraints in the form
.
Determine the appropriate number of action variables and express the
differential constraints in the form
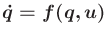 .
.
- Introduce a phase space and convert
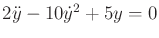 into the form
into the form
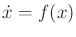 .
.
- Introduce a phase space and convert
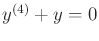 into the
form
into the
form
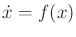 .
.
- Derive the configuration transition equation
(13.19) for a car pulling trailers.
- Use the main idea of Section 13.2.4 to develop a
smooth-steering extension of the car pulling trailers,
(13.19).
- Suppose that two identical differential-drive robots are
connected together at their centers with a rigid bar of length
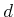 .
The robots are attached at each end of the rod, and each attachment
forms a revolute joint. There are four wheels to control; however,
some combinations of wheel rotations cause skidding. Assuming that
skidding is not allowed, develop a motion model of the form
.
The robots are attached at each end of the rod, and each attachment
forms a revolute joint. There are four wheels to control; however,
some combinations of wheel rotations cause skidding. Assuming that
skidding is not allowed, develop a motion model of the form
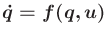 , in which
, in which  and
and 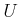 are chosen to reflect the true degrees
of freedom.
are chosen to reflect the true degrees
of freedom.
- Extend the lunar lander model to a general rigid body with a
thruster that does not apply forces through the center of mass.
- Develop a model for a 3D rotating rigid body fired out of a
canon at a specified angle above level ground under gravity. Suppose
that thrusters are placed on the body, enabling it to be controlled
before it impacts the ground. Develop general phase transition
equations.
- Add gravity with respect to
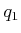 in Example 13.12
and derive the new state transition equation using the Euler-Lagrange equation.
in Example 13.12
and derive the new state transition equation using the Euler-Lagrange equation.
- Use the constrained Lagrangian to derive the equations of motion
of the pendulum in Example 13.8.
Figure 13.14:
A double pendulum.
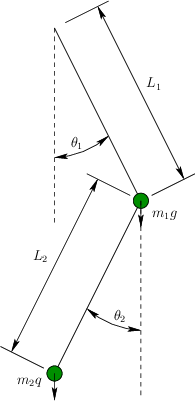 |
- Define a phase space, and determine an equation of the form
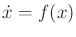 for the double pendulum shown
in Figure 13.14.
for the double pendulum shown
in Figure 13.14.
- Extend Example 13.13 to obtain the dynamics of a
three-link manipulator. The third link,
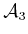 , is attached to the
other two by a revolute joint. The new parameters are
, is attached to the
other two by a revolute joint. The new parameters are 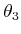 ,
,
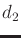 ,
, 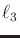 ,
, 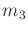 , and
, and 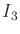 .
.
- Solve Example 13.14 by parameterizing the sphere
with standard spherical coordinates and using the unconstrained
Lagrangian. Verify that the same answer is obtained.
- Convert the equations in
(13.161) into phase space form, to obtain the phase
transition equation in the form
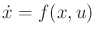 . Express the right
side of the equation in terms of the basic parameters, such as mass,
moment of inertia, and lengths.
. Express the right
side of the equation in terms of the basic parameters, such as mass,
moment of inertia, and lengths.
- Define the Hamiltonian for a free-floating 2D rigid body under
gravity and develop Hamilton's equations.
Implementations
- Make a 3D spacecraft (rigid-body) simulator that allows any
number of binary thrusters to be placed in any position and
orientation.
- Make a simulator for the two-link manipulator in Example
13.13.
Steven M LaValle
2020-08-14
