The Lagrangian formulation of Section 13.4.1 can be
extended to allow additional constraints placed on 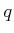 and
and 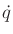 .
This is very powerful for developing state transition equations for
robots that have closed kinematic chains or wheeled bodies. If there
are closed chains, then the configurations may be restricted to lie in
a subset of
.
This is very powerful for developing state transition equations for
robots that have closed kinematic chains or wheeled bodies. If there
are closed chains, then the configurations may be restricted to lie in
a subset of  . If a parameterization of the solution set is
possible, then
. If a parameterization of the solution set is
possible, then  can be redefined over the reduced C-space. This
is usually not possible, however, because such a parametrization is
difficult to obtain, as mentioned in Section 4.4. If
there are wheels or other contact-based constraints, such as those in
Section 13.1.3, then extra constraints on
can be redefined over the reduced C-space. This
is usually not possible, however, because such a parametrization is
difficult to obtain, as mentioned in Section 4.4. If
there are wheels or other contact-based constraints, such as those in
Section 13.1.3, then extra constraints on 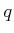 and
and 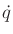 exist. Dynamics can be incorporated into the models of Section
13.1 by extending the Euler-Lagrange equation.
exist. Dynamics can be incorporated into the models of Section
13.1 by extending the Euler-Lagrange equation.
The coming method will be based on Lagrange multipliers. Recall from
standard calculus that to optimize a function 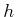 defined over
defined over
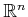 , subject to an implicit constraint
, subject to an implicit constraint 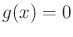 , it is
sufficient to consider only the extrema of
, it is
sufficient to consider only the extrema of
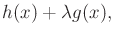 |
(13.162) |
in which
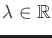 represents a Lagrange multiplier
[508]. The extrema are found by solving
represents a Lagrange multiplier
[508]. The extrema are found by solving
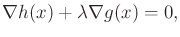 |
(13.163) |
which expresses  equations of the form
equations of the form
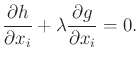 |
(13.164) |
The same principle applies for handling velocity constraints on  .
.
Suppose that there are velocity constraints on  as considered in
Section 13.1. Consider implicit constraints, in which
there are
as considered in
Section 13.1. Consider implicit constraints, in which
there are  equations of the form
equations of the form
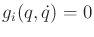 for
for 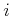 from
from
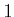 to
to  . Parametric constraints can be handled as a special case
of implicit constraints by writing
. Parametric constraints can be handled as a special case
of implicit constraints by writing
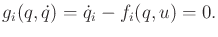 |
(13.165) |
For any constraints that contain actions 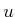 , no extra difficulties
arise. Each
, no extra difficulties
arise. Each 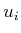 is treated as a constant in the following analysis.
Therefore, action variables will not be explicitly named in the
expressions.
is treated as a constant in the following analysis.
Therefore, action variables will not be explicitly named in the
expressions.
As before, assume time-invariant dynamics (see [789] for the
time-varying case). Starting with
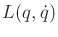 defined using
(13.130), let the new criterion be
defined using
(13.130), let the new criterion be
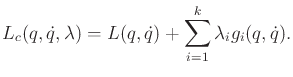 |
(13.166) |
A functional 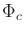 is defined by substituting
is defined by substituting 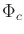 for
for 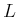 in
(13.114).
in
(13.114).
The extremals of 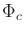 are given by
are given by  equations,
equations,
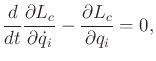 |
(13.167) |
and  equations,
equations,
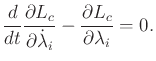 |
(13.168) |
The justification for this is the same as for
(13.124), except now 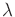 is included. The
equations of (13.168) are equivalent to the constraints
is included. The
equations of (13.168) are equivalent to the constraints
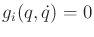 . The first term of each is zero because
. The first term of each is zero because
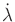 does not appear in the constraints, which reduces them to
does not appear in the constraints, which reduces them to
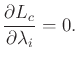 |
(13.169) |
This already follows from the constraints on extremals of 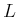 and the
constraints
and the
constraints
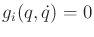 . In (13.167), there are
. In (13.167), there are  equations in
equations in 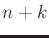 unknowns. The
unknowns. The  Lagrange multipliers can be
eliminated by using the
Lagrange multipliers can be
eliminated by using the  constraints
constraints
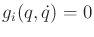 . This
corresponds to Lagrange multiplier elimination in standard constrained
optimization [508].
. This
corresponds to Lagrange multiplier elimination in standard constrained
optimization [508].
The expressions in (13.167) and the constraints
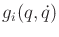 may be quite complicated, which makes the determination
of a state transition equation challenging. General forms are given
in Section 3.8 of [789]. An important special case will be
considered here. Suppose that the constraints are Pfaffian,
may be quite complicated, which makes the determination
of a state transition equation challenging. General forms are given
in Section 3.8 of [789]. An important special case will be
considered here. Suppose that the constraints are Pfaffian,
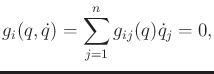 |
(13.170) |
as introduced in Section 13.1. This includes the
nonholonomic velocity constraints due to wheeled vehicles, which were
presented in Section 13.1.2. Furthermore, this includes
the special case of constraints of the form
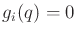 , which models
closed kinematic chains. Such constraints can be differentiated with
respect to time to obtain
, which models
closed kinematic chains. Such constraints can be differentiated with
respect to time to obtain
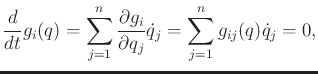 |
(13.171) |
which is in the Pfaffian form. This enables the dynamics of closed
chains, considered in Section 4.4, to be expressed
without even having a parametrization of the subset of  that
satisfies the closure constraints. Starting in implicit form,
differentiation is required to convert them into the Pfaffian form.
that
satisfies the closure constraints. Starting in implicit form,
differentiation is required to convert them into the Pfaffian form.
For the important case of Pfaffian constraints, (13.167) simplifies to
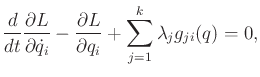 |
(13.172) |
The Pfaffian constraints can be used to eliminate the Lagrange
multipliers, if desired. Note that 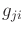 represents the
represents the 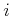 th term
of the
th term
of the 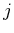 th Pfaffian constraint. An action variable
th Pfaffian constraint. An action variable 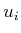 can be
placed on the right side of each constraint, if desired.
can be
placed on the right side of each constraint, if desired.
Equation (13.172) often appears instead as
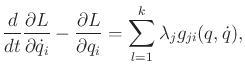 |
(13.173) |
which is an alternative but equivalent expression of constraints
because the Lagrange multipliers can be negated without affecting the
existence of extremals. In this case, a nice interpretation due to
D'Alembert can be given. Expressions that appear on the right
of (13.173) can be considered as actions, as mentioned in
Section 13.4.1. As stated previously, such actions are
called generalized forces in mechanics. The principle of
virtual work is obtained by integrating the reaction forces needed to
maintain the constraints. These reaction forces are precisely given
on the right side of (13.173). Due to the cancellation of
forces, no true work is done by the constraints (if there is no
friction).
Example 13..14 (A Particle on a Sphere)
Suppose that a particle travels on a unit sphere without friction or
gravity. Let
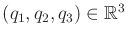
denote the position of the
point. The Lagrangian function
is the kinetic energy
,
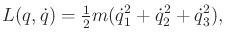 |
(13.174) |
in which
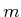
is the particle mass. For simplicity, assume that
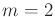
.
The constraint that the particle must travel on a sphere yields
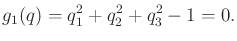 |
(13.175) |
This can be put into Pfaffian
form by time
differentiation to obtain
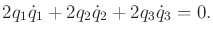 |
(13.176) |
Since
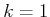
, there is a single Lagrange multiplier
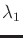
.
Applying (
13.172) yields three equations,
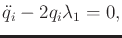 |
(13.177) |
for
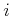
from
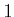
to
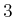
. The generic form of the solution is
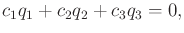 |
(13.178) |
in which the
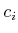
are real-valued constants that can be determined
from the initial position of the particle. This represents the
equation of a plane through the origin. The intersection of the plane
with the sphere is a great circle. This implies that the particle
moves between two points by traveling along the great circle. These
are the shortest paths (geodesics) on the sphere.

The general forms in Section 13.4.2 can be extended to the
constrained case. For example, (13.142) generalizes to
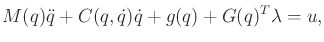 |
(13.179) |
in which 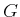 is a
is a
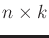 matrix that represents all of the
matrix that represents all of the
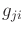 Pfaffian coefficients. In this case, the Lagrange
multipliers can be computed as [725]
Pfaffian coefficients. In this case, the Lagrange
multipliers can be computed as [725]
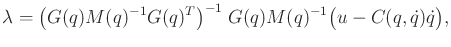 |
(13.180) |
assuming 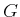 is time-invariant.
is time-invariant.
The phase transition equation can be determined in the usual way by
performing the required differentiations, defining the 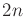 phase
variables, and solving for
phase
variables, and solving for 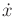 . The result generalizes
(13.148).
. The result generalizes
(13.148).
Steven M LaValle
2020-08-14

![]() and
and ![]() .
This is very powerful for developing state transition equations for
robots that have closed kinematic chains or wheeled bodies. If there
are closed chains, then the configurations may be restricted to lie in
a subset of
.
This is very powerful for developing state transition equations for
robots that have closed kinematic chains or wheeled bodies. If there
are closed chains, then the configurations may be restricted to lie in
a subset of ![]() . If a parameterization of the solution set is
possible, then
. If a parameterization of the solution set is
possible, then ![]() can be redefined over the reduced C-space. This
is usually not possible, however, because such a parametrization is
difficult to obtain, as mentioned in Section 4.4. If
there are wheels or other contact-based constraints, such as those in
Section 13.1.3, then extra constraints on
can be redefined over the reduced C-space. This
is usually not possible, however, because such a parametrization is
difficult to obtain, as mentioned in Section 4.4. If
there are wheels or other contact-based constraints, such as those in
Section 13.1.3, then extra constraints on ![]() and
and ![]() exist. Dynamics can be incorporated into the models of Section
13.1 by extending the Euler-Lagrange equation.
exist. Dynamics can be incorporated into the models of Section
13.1 by extending the Euler-Lagrange equation.
![]() defined over
defined over
![]() , subject to an implicit constraint
, subject to an implicit constraint ![]() , it is
sufficient to consider only the extrema of
, it is
sufficient to consider only the extrema of
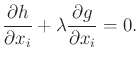
![]() as considered in
Section 13.1. Consider implicit constraints, in which
there are
as considered in
Section 13.1. Consider implicit constraints, in which
there are ![]() equations of the form
equations of the form
![]() for
for ![]() from
from
![]() to
to ![]() . Parametric constraints can be handled as a special case
of implicit constraints by writing
. Parametric constraints can be handled as a special case
of implicit constraints by writing
![]() defined using
(13.130), let the new criterion be
defined using
(13.130), let the new criterion be
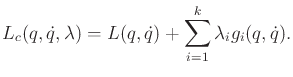
![]() are given by
are given by ![]() equations,
equations,
![]() may be quite complicated, which makes the determination
of a state transition equation challenging. General forms are given
in Section 3.8 of [789]. An important special case will be
considered here. Suppose that the constraints are Pfaffian,
may be quite complicated, which makes the determination
of a state transition equation challenging. General forms are given
in Section 3.8 of [789]. An important special case will be
considered here. Suppose that the constraints are Pfaffian,
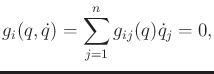
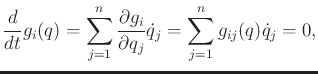
![]() phase
variables, and solving for
phase
variables, and solving for ![]() . The result generalizes
(13.148).
. The result generalizes
(13.148).