
Next: 11.4.3 Derived Information Spaces Up: 11.4 Continuous State Spaces Previous: 11.4.1 Discrete-Stage Information Spaces
Now assume that there is a continuum of stages. Most of the
components of Section 11.4.1 remain the same. The spaces ![]() ,
,
![]() ,
, ![]() ,
, ![]() , and
, and
![]() remain the same. The sensor
mapping also remains the same. The main difference occurs in the
state transition equation because the effect of nature must be
expressed in terms of velocities. This was already introduced in
Section 10.6. In that context, there was only uncertainty
in predictability. In the current context there may be uncertainties
in both predictability and in sensing the current state.
remain the same. The sensor
mapping also remains the same. The main difference occurs in the
state transition equation because the effect of nature must be
expressed in terms of velocities. This was already introduced in
Section 10.6. In that context, there was only uncertainty
in predictability. In the current context there may be uncertainties
in both predictability and in sensing the current state.
For the discrete-stage case, the history I-states were based on action
and observation sequences. For the continuous-time case, the history
instead becomes a function of time. As defined in Section
7.1.1, let ![]() denote a time interval, which may
be bounded or unbounded. Let
denote a time interval, which may
be bounded or unbounded. Let
![]() be
called the observation history up to time
be
called the observation history up to time ![]() . Similarly,
let
. Similarly,
let
![]() and
and
![]() be called the action history and state history,
respectively, up to time
be called the action history and state history,
respectively, up to time ![]() .
.
Thus, the three kinds of sensor mappings in the continuous-time case are as follows:
If
![]() and
and
![]() are combined with the initial condition
are combined with the initial condition
![]() , the history I-state at time
, the history I-state at time ![]() is obtained as
is obtained as
| (11.53) |
A continuous-time version of the cost functional in Formulation
11.1 can be given to evaluate the execution of a plan. Let
![]() denote a cost functional that may be applied to any state-action
history
denote a cost functional that may be applied to any state-action
history
![]() to yield
to yield
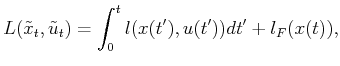 |
(11.55) |
Steven M LaValle 2020-08-14