The history I-space is simply the set of all possible history
I-states. Although the history I-states appear to be quite
complicated, it is helpful to think of them abstractly as points in a
new space. To define the set of all possible history I-states, the
sets of all initial conditions, actions, and observations must be
precisely defined.
The set of all observation histories is denoted as
 and
is obtained by a Cartesian product of
and
is obtained by a Cartesian product of  copies of the observation
space:
copies of the observation
space:
 |
(11.16) |
Similarly, the set of all action histories is
 , the
Cartesian product of
, the
Cartesian product of 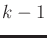 copies of the action space
copies of the action space 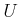 .
.
It is slightly more complicated to define the set of all possible
initial conditions because three different types of initial conditions
are possible. Let
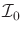 denote the initial condition space.
Depending on which of the three types of initial conditions are used,
one of the following three definitions of
denote the initial condition space.
Depending on which of the three types of initial conditions are used,
one of the following three definitions of
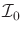 is used:
is used:
- Known State: If the initial state,
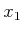 , is given, then
, is given, then
 . Typically,
. Typically,
 ; however, it might be known
in some instances that certain initial states are impossible.
Therefore, it is generally written that
; however, it might be known
in some instances that certain initial states are impossible.
Therefore, it is generally written that
 .
.
- Nondeterministic: If
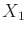 is given, then
is given, then
 (the power set of
(the power set of  ). Again, a typical situation is
). Again, a typical situation is
 ; however, it might be known that certain subsets of
; however, it might be known that certain subsets of  are
impossible as initial conditions.
are
impossible as initial conditions.
- Probabilistic: Finally, if
 is given, then
is given, then
 , in which
, in which
 is the set of all probability
distributions over
is the set of all probability
distributions over  .
.
The history I-space at stage  is expressed as
is expressed as
 |
(11.17) |
Each
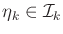 yields an initial condition, an action
history, and an observation history. It will be convenient to
consider I-spaces that do not depend on
yields an initial condition, an action
history, and an observation history. It will be convenient to
consider I-spaces that do not depend on  . This will be defined by
taking a union (be careful not to mistakenly think of this
construction as a Cartesian product). If there are
. This will be defined by
taking a union (be careful not to mistakenly think of this
construction as a Cartesian product). If there are 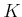 stages, then
the history I-space is
stages, then
the history I-space is
 |
(11.18) |
Most often, the number of stages is not fixed. In this case,
 is defined to be the union of
is defined to be the union of
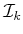 over all
over all
 :
:
 |
(11.19) |
This construction is related to the state space obtained for
time-varying motion planning in Section 7.1. The
history I-space is stage-dependent because information accumulates
over time. In the discrete model, the reference to time is only
implicit through the use of stages. Therefore, stage-dependent
I-spaces are defined. Taking the union of all of these is similar to
the state space that was formed in Section 7.1 by making
time be one axis of the state space. For the history I-space,
 , the stage index
, the stage index  can be imagined as an ``axis.''
can be imagined as an ``axis.''
One immediate concern regarding the history I-space
 is
that its I-states may be arbitrarily long because the history grows
linearly with the number of stages. For now, it is helpful to imagine
is
that its I-states may be arbitrarily long because the history grows
linearly with the number of stages. For now, it is helpful to imagine
 abstractly as another kind of state space, without paying
close attention to how complicated each
abstractly as another kind of state space, without paying
close attention to how complicated each
 may be to
represent. In many contexts, there are ways to simplify the I-space.
This is the topic of Section 11.2.
may be to
represent. In many contexts, there are ways to simplify the I-space.
This is the topic of Section 11.2.
Steven M LaValle
2020-08-14

![]() and
is obtained by a Cartesian product of
and
is obtained by a Cartesian product of ![]() copies of the observation
space:
copies of the observation
space:
![]() denote the initial condition space.
Depending on which of the three types of initial conditions are used,
one of the following three definitions of
denote the initial condition space.
Depending on which of the three types of initial conditions are used,
one of the following three definitions of
![]() is used:
is used:
![]() is expressed as
is expressed as
![]() is
that its I-states may be arbitrarily long because the history grows
linearly with the number of stages. For now, it is helpful to imagine
is
that its I-states may be arbitrarily long because the history grows
linearly with the number of stages. For now, it is helpful to imagine
![]() abstractly as another kind of state space, without paying
close attention to how complicated each
abstractly as another kind of state space, without paying
close attention to how complicated each
![]() may be to
represent. In many contexts, there are ways to simplify the I-space.
This is the topic of Section 11.2.
may be to
represent. In many contexts, there are ways to simplify the I-space.
This is the topic of Section 11.2.