
Next: 2.3.3 Dijkstra Revisited Up: 2.3 Discrete Optimal Planning Previous: 2.3.1.2 Forward value iteration
The value-iteration
method for fixed-length plans can be generalized nicely to the case in
which plans of different lengths are allowed. There will be no bound
on the maximal length of a plan; therefore, the current case is truly
a generalization of Formulation 2.1 because arbitrarily long
plans may be attempted in efforts to reach ![]() . The model for
the general case does not require the specification of
. The model for
the general case does not require the specification of ![]() but
instead introduces a special action,
but
instead introduces a special action, ![]() .
.
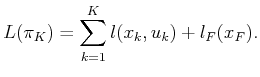 |
(2.17) |
The termination action is the key to allowing plans of different
lengths. It will appear throughout this book. Suppose that value
iterations are performed up to ![]() , and for the problem there exists
a two-step solution plan,
, and for the problem there exists
a two-step solution plan, ![]() , that arrives in
, that arrives in ![]() from
from
![]() . This plan is equivalent to the five-step plan
. This plan is equivalent to the five-step plan
![]() because the termination action does not change
the state, nor does it accumulate cost. The resulting five-step plan
reaches
because the termination action does not change
the state, nor does it accumulate cost. The resulting five-step plan
reaches ![]() and costs the same as
and costs the same as ![]() . With this simple
extension, the forward and backward value iteration methods of Section
2.3.1 may be applied for any fixed
. With this simple
extension, the forward and backward value iteration methods of Section
2.3.1 may be applied for any fixed ![]() to optimize over all
plans of length
to optimize over all
plans of length ![]() or less (instead of fixing
or less (instead of fixing ![]() ).
).
The next step is to remove the dependency on ![]() . Consider running
backward value iterations indefinitely. At some point,
. Consider running
backward value iterations indefinitely. At some point, ![]() will
be computed, but there is no reason why the process cannot be
continued onward to
will
be computed, but there is no reason why the process cannot be
continued onward to ![]() ,
, ![]() , and so on. Recall that
, and so on. Recall that
![]() is not utilized in the backward value-iteration method;
therefore, there is no concern regarding the starting initial state of
the plans. Suppose that backward value iteration was applied for
is not utilized in the backward value-iteration method;
therefore, there is no concern regarding the starting initial state of
the plans. Suppose that backward value iteration was applied for ![]() and was executed down to
and was executed down to ![]() . This considers all plans
of length
. This considers all plans
of length ![]() or less. Note that it is harmless to add
or less. Note that it is harmless to add ![]() to all
stage indices to shift all of the cost-to-go functions. Instead of
running from
to all
stage indices to shift all of the cost-to-go functions. Instead of
running from ![]() to
to ![]() , they can run from
, they can run from ![]() to
to ![]() without affecting their values. The index shifting is
allowed because none of the costs depend on the particular index that
is given to the stage. The only important aspect of the value
iterations is that they proceed backward and consecutively from stage
to stage.
without affecting their values. The index shifting is
allowed because none of the costs depend on the particular index that
is given to the stage. The only important aspect of the value
iterations is that they proceed backward and consecutively from stage
to stage.
Eventually, enough iterations will have been executed so that an
optimal plan is known from every state that can reach ![]() . From
that stage, say
. From
that stage, say ![]() , onward, the cost-to-go values from one value
iteration to the next will be stationary, meaning that for all
, onward, the cost-to-go values from one value
iteration to the next will be stationary, meaning that for all ![]() ,
,
![]() for all
for all ![]() . Once the stationary condition is
reached, the cost-to-go function no longer depends on a particular
stage
. Once the stationary condition is
reached, the cost-to-go function no longer depends on a particular
stage ![]() . In this case, the stage index may be dropped, and the
recurrence becomes
. In this case, the stage index may be dropped, and the
recurrence becomes
Are there any conditions under which backward value iterations could
be executed forever, with each iteration producing a cost-to-go
function for which some values are different from the previous
iteration? If ![]() is nonnegative for all
is nonnegative for all ![]() and
and
![]() , then this could never happen. It could certainly be true that,
for any fixed
, then this could never happen. It could certainly be true that,
for any fixed ![]() , longer plans will exist, but this cannot be said of
optimal plans. From every
, longer plans will exist, but this cannot be said of
optimal plans. From every ![]() , there either exists a plan
that reaches
, there either exists a plan
that reaches ![]() with finite cost or there is no solution. For
each state from which there exists a plan that reaches
with finite cost or there is no solution. For
each state from which there exists a plan that reaches ![]() ,
consider the number of stages in the optimal plan. Consider the
maximum number of stages taken from all states that can reach
,
consider the number of stages in the optimal plan. Consider the
maximum number of stages taken from all states that can reach
![]() . This serves as an upper bound on the number of value
iterations before the cost-to-go becomes stationary. Any further
iterations will just consider solutions that are worse than the ones
already considered (some may be equivalent due to the termination
action and shifting of stages). Some trouble might occur if
. This serves as an upper bound on the number of value
iterations before the cost-to-go becomes stationary. Any further
iterations will just consider solutions that are worse than the ones
already considered (some may be equivalent due to the termination
action and shifting of stages). Some trouble might occur if ![]() contains negative values. If the state transition graph contains a
cycle for which total cost is negative, then it is preferable to
execute a plan that travels around the cycle forever, thereby reducing
the total cost to
contains negative values. If the state transition graph contains a
cycle for which total cost is negative, then it is preferable to
execute a plan that travels around the cycle forever, thereby reducing
the total cost to ![]() . Therefore, we will assume that the cost
functional is defined in a sensible way so that negative cycles do not
exist. Otherwise, the optimization model itself appears flawed. Some
negative values for
. Therefore, we will assume that the cost
functional is defined in a sensible way so that negative cycles do not
exist. Otherwise, the optimization model itself appears flawed. Some
negative values for ![]() , however, are allowed as long as there
are no negative cycles. (It is straightforward to detect and report
negative cycles before running the value iterations.)
, however, are allowed as long as there
are no negative cycles. (It is straightforward to detect and report
negative cycles before running the value iterations.)
Since the particular stage index is unimportant, let ![]() be the
index of the final stage, which is the stage at which the backward
value iterations begin. Hence,
be the
index of the final stage, which is the stage at which the backward
value iterations begin. Hence, ![]() is the final stage cost,
which is obtained directly from
is the final stage cost,
which is obtained directly from ![]() . Let
. Let ![]() denote the stage
index at which the cost-to-go values all become stationary. At this
stage, the optimal cost-to-go function,
denote the stage
index at which the cost-to-go values all become stationary. At this
stage, the optimal cost-to-go function,
![]() , is expressed by assigning
, is expressed by assigning
![]() . In
other words, the particular stage index no longer matters. The value
. In
other words, the particular stage index no longer matters. The value
![]() gives the optimal cost to go from state
gives the optimal cost to go from state ![]() to the
specific goal state
to the
specific goal state ![]() .
.
If the optimal actions are not stored during the value iterations, the
optimal cost-to-go, ![]() , can be used to efficiently recover them.
Consider starting from some
, can be used to efficiently recover them.
Consider starting from some ![]() . What is the optimal next
action? This is given by
. What is the optimal next
action? This is given by
As in the case of fixed-length plans, the direction of the value
iterations can be reversed to obtain a forward value-iteration method
for the variable-length planning problem. In this case, the backward
state transition equation, ![]() , is used once again. Also, the
initial cost term
, is used once again. Also, the
initial cost term ![]() is used instead of
is used instead of ![]() , as in
(2.14). The forward value-iteration method starts at
, as in
(2.14). The forward value-iteration method starts at ![]() ,
and then iterates until the cost-to-come becomes stationary. Once
again, the termination action,
,
and then iterates until the cost-to-come becomes stationary. Once
again, the termination action, ![]() , preserves the cost of plans that
arrived at a state in earlier iterations. Note that it is not
required to specify
, preserves the cost of plans that
arrived at a state in earlier iterations. Note that it is not
required to specify ![]() . A counterpart to
. A counterpart to ![]() may be
obtained, from which optimal actions can be recovered. When the
cost-to-come values become stationary, an optimal cost-to-come
function,
may be
obtained, from which optimal actions can be recovered. When the
cost-to-come values become stationary, an optimal cost-to-come
function,
![]() , may be
expressed by assigning
, may be
expressed by assigning
![]() , in which
, in which ![]() is the final
stage reached when the algorithm terminates. The value
is the final
stage reached when the algorithm terminates. The value ![]() gives the cost of an optimal plan that starts from
gives the cost of an optimal plan that starts from ![]() and
reaches
and
reaches ![]() . The optimal action sequence for any specified goal
. The optimal action sequence for any specified goal
![]() can be obtained using
can be obtained using
 |
 |
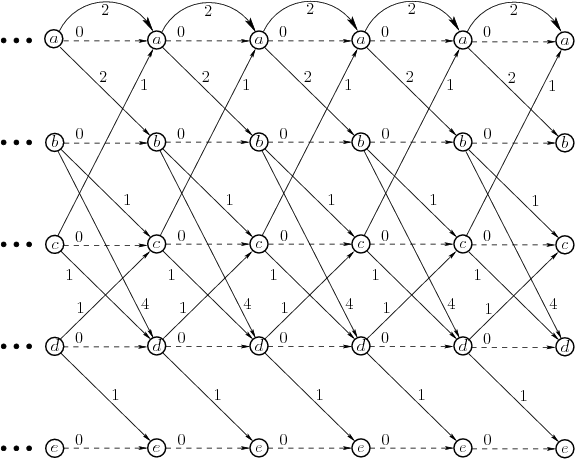
See Figure 2.14. After a few backward value iterations,
the cost-to-go values become stationary. After this point, the
termination action is being applied from all reachable states and no
further cost accumulates. The final cost-to-go function is defined to
be ![]() . Since
. Since ![]() is not reachable from
is not reachable from ![]() ,
,
![]() .
.
As an example of using (2.19) to recover optimal actions,
consider starting from state ![]() . The action that leads to
. The action that leads to ![]() is
chosen next because the total cost
is
chosen next because the total cost
![]() is better than
is better than
![]() (the
(the ![]() comes from the action cost). From state
comes from the action cost). From state
![]() , the optimal action leads to
, the optimal action leads to ![]() , which produces total cost
, which produces total cost
![]() . Similarly, the next action leads to
. Similarly, the next action leads to
![]() , which
terminates the plan.
, which
terminates the plan.
 |
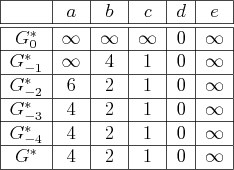
Using forward value iteration, suppose that
![]() . The
following cost-to-come functions shown in Figure 2.15 are
obtained. For any finite value that remains constant from one
iteration to the next, the termination action was applied. Note that
the last value iteration is useless in this example. Once
. The
following cost-to-come functions shown in Figure 2.15 are
obtained. For any finite value that remains constant from one
iteration to the next, the termination action was applied. Note that
the last value iteration is useless in this example. Once ![]() is computed, the optimal cost-to-come to every possible state from
is computed, the optimal cost-to-come to every possible state from
![]() is determined, and future cost-to-come functions are
identical. Therefore, the final cost-to-come is renamed
is determined, and future cost-to-come functions are
identical. Therefore, the final cost-to-come is renamed ![]() .
.
![]()
Steven M LaValle 2020-08-14