Under this model, the history I-state is truncated. Any actions or
observations received earlier than 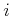 stages ago are dropped from
memory. An I-map,
stages ago are dropped from
memory. An I-map,
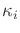 , is defined as
, is defined as
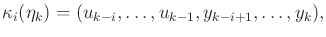 |
(11.41) |
for any integer 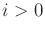 and
and 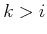 . If
. If 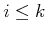 , then the derived
I-state is the full history I-state, (11.14). The
advantage of this approach, if it leads to a solution, is that the
length of the I-state no longer grows with the number of stages. If
, then the derived
I-state is the full history I-state, (11.14). The
advantage of this approach, if it leads to a solution, is that the
length of the I-state no longer grows with the number of stages. If
 and
and 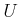 are finite, then the derived I-space is also finite. Note
that
are finite, then the derived I-space is also finite. Note
that
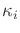 is sufficient in the sense defined in Section
11.2.1 because enough history is passed from stage to stage
to determine the derived I-states.
is sufficient in the sense defined in Section
11.2.1 because enough history is passed from stage to stage
to determine the derived I-states.
Steven M LaValle
2020-08-14

![]() stages ago are dropped from
memory. An I-map,
stages ago are dropped from
memory. An I-map,
![]() , is defined as
, is defined as