
Next: Making smaller information-feedback plans Up: 11.2 Derived Information Spaces Previous: 11.2 Derived Information Spaces
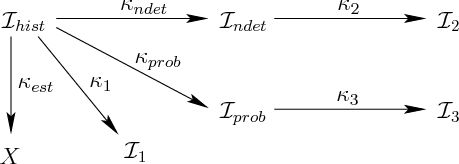 |
Consider a function that maps the history I-space into a space that is
simpler to manage. Formally, let
![]() denote a function from a history I-space,
denote a function from a history I-space,
![]() , to a
derived I-space,
, to a
derived I-space,
![]() .
The function,
.
The function, ![]() , is called an information mapping, or I-map. The derived I-space may be any set; hence, there is great
flexibility in defining an I-map.11.2 Figure 11.3 illustrates the idea.
The starting place is
, is called an information mapping, or I-map. The derived I-space may be any set; hence, there is great
flexibility in defining an I-map.11.2 Figure 11.3 illustrates the idea.
The starting place is
![]() , and mappings are made to various
derived I-spaces. Some generic mappings,
, and mappings are made to various
derived I-spaces. Some generic mappings,
![]() ,
,
![]() , and
, and
![]() , are shown, along with some very important kinds,
, are shown, along with some very important kinds,
![]() ,
,
![]() and
and
![]() . The last two are the subjects of Sections
11.2.2 and 11.2.3, respectively. The other important
I-map is
. The last two are the subjects of Sections
11.2.2 and 11.2.3, respectively. The other important
I-map is
![]() , which uses the history to estimate the state;
hence, the derived I-space is
, which uses the history to estimate the state;
hence, the derived I-space is ![]() (see Example 11.11).
In general, an I-map can even map any derived I-space to another,
yielding
(see Example 11.11).
In general, an I-map can even map any derived I-space to another,
yielding
![]() , for any I-spaces
, for any I-spaces
![]() and
and
![]() . Note that any composition of I-maps yields
an I-map. The derived I-spaces
. Note that any composition of I-maps yields
an I-map. The derived I-spaces
![]() and
and
![]() from Figure
11.3 are obtained via compositions.
from Figure
11.3 are obtained via compositions.