- Show that
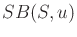 cannot be expressed as the union of all
cannot be expressed as the union of all
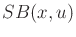 for
for 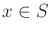 .
.
- Show that for any
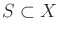 and any state transition
equation,
and any state transition
equation,
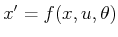 , it follows that
, it follows that
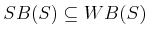 .
.
- Generalize the strong and weak backprojections of Section
10.1.2 to work for multiple stages.
- Assume that nondeterministic uncertainty is used, and there is
no limit on the number of stages. Determine an expression for the
forward projection at any stage
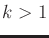 , given that
, given that 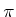 is
applied.
is
applied.
- Give an algorithm for computing nondeterministic forward
projections that uses matrices with binary entries. What is the
asymptotic running time and space for your algorithm?
- Develop a variant of the algorithm in Figure 10.6
that is based on possibly achieving the goal, as opposed to guaranteeing that it is achieved.
- Develop a forward version of value
iteration for nondeterministic uncertainty, by paralleling the
derivation in Section 10.2.1.
- Do the same as in Exercise
7, but for probabilistic uncertainty.
- Give an algorithm that computes
probabilistic forward projections directly from the plan-based state
transition graph,
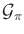 .
.
- Augment the nondeterministic value-iteration
method of Section 10.2.1 to detect and handle states from
which the goal is possibly reachable but not guaranteed
reachable.
- Derive a generalization of
(10.39) for the case of stage-dependent
state-transition equations,
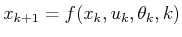 , and cost
terms,
, and cost
terms,
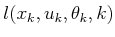 , under nondeterministic uncertainty.
, under nondeterministic uncertainty.
- Do the same as in Exercise 11, but for
probabilistic uncertainty.
- Extend the policy-iteration method of
Figure 10.4 to work for the more general case of
nature-dependent cost terms,
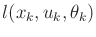 .
.
- Derive a policy-iteration method that is the
nondeterministic analog to the method in Figure 10.4.
Assume that the cost terms do not depend on nature.
- Can policy iteration be applied to solve problems under
Formulation 2.3, which involve no uncertainties? Explain
what happens in this case.
- Show that the probabilistic infinite-horizon problem under the
discounted-cost model is equivalent in terms of cost-to-go to a
particular stochastic shortest-path problem (under Formulation
10.1). [Hint: See page 378 of [95].]
- Derive a value-iteration method for the
infinite-horizon problem with the discounted-cost model and
nondeterministic uncertainty. This method should compute the
cost-to-go given in (10.71).
Figure 10.23:
A two-player, two-stage game expressed
using a game tree.
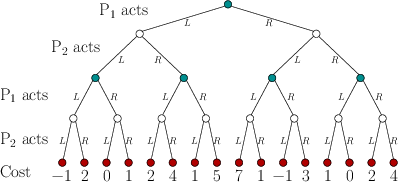 |
- Figure 10.23 shows a two-stage,
zero-sum game expressed as a game tree. Compute the randomized value
of this sequential game and give the corresponding randomized security
plans for each player.
- Generalize alpha-beta pruning beyond game trees so that it works
for sequential games defined on a state space, starting from a fixed
initial state.
- Derive (10.110) and (10.111).
- Extend Formulation 2.4 to allow nondeterministic
uncertainty. This can be accomplished by specifying sets of possible
effects of operators.
- Extend Formulation 2.4 to allow probabilistic
uncertainty. For this case, assign probabilities to the possible
operator effects.
Implementations
- Implement probabilistic backward value iteration and study the
convergence issue depicted in Figure 10.3. How does this
affect performance in problems for which there are many cycles in the
state transition graph? How does performance depend on particular
costs and transition probabilities?
- Implement the nondeterministic version of Dijkstra's algorithm
and test it on a few examples.
- Implement and test the probabilistic version of Dijkstra's
algorithm. Make sure that the condition
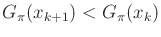 from 10.2.3 is satisfied. Study the
performance of the algorithm on problems for which the condition is
almost violated.
from 10.2.3 is satisfied. Study the
performance of the algorithm on problems for which the condition is
almost violated.
- Experiment with the simulation-based version of value iteration,
which is given by (10.101). For some simple examples,
characterize how the performance depends on the choice of
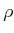 .
.
- Implement a recursive algorithm that uses dynamic programming to
determine the upper and lower values for a sequential game expressed
using a game tree under the stage-by-stage model.
Steven M LaValle
2020-08-14
