
Next: 10.1.2 Forward Projections and Up: 10.1 Introducing Sequential Games Previous: 10.1 Introducing Sequential Games
The formulation presented in this section is an extension of
Formulation 2.3 that incorporates the effects of nature at
every stage. Let ![]() denote a discrete state space, and let
denote a discrete state space, and let ![]() denote the set of actions available to the decision maker (or robot)
from state
denote the set of actions available to the decision maker (or robot)
from state ![]() . At each stage
. At each stage ![]() it is assumed that a nature action
it is assumed that a nature action ![]() is chosen from a set
is chosen from a set
![]() .
This can be considered as a multi-stage generalization of Formulation
9.4, which introduced
.
This can be considered as a multi-stage generalization of Formulation
9.4, which introduced ![]() . Now
. Now ![]() may
depend on the state in addition to the action because both
may
depend on the state in addition to the action because both ![]() and
and
![]() are available in the current setting. This implies that nature
acts with the knowledge of the action selected by the decision maker.
It is always assumed that during stage
are available in the current setting. This implies that nature
acts with the knowledge of the action selected by the decision maker.
It is always assumed that during stage ![]() , the decision maker does
not know the particular nature action that will be chosen. It does,
however, know the set
, the decision maker does
not know the particular nature action that will be chosen. It does,
however, know the set
![]() for all
for all ![]() and
and
![]() .
.
As in Section 9.2, there are two alternative nature
models: nondeterministic or probabilistic. If the nondeterministic
model is used, then it is only known that nature will make a choice
from
![]() . In this case, making decisions using
worst-case analysis is appropriate.
. In this case, making decisions using
worst-case analysis is appropriate.
If the probabilistic model is used, then a probability distribution
over
![]() is specified as part of the model. The most
important assumption to keep in mind for this case is that nature is
Markovian. In general, this means that the probability depends
only on local information. In most applications, this locality is
with respect to time. In our formulation, it means that the
distribution over
is specified as part of the model. The most
important assumption to keep in mind for this case is that nature is
Markovian. In general, this means that the probability depends
only on local information. In most applications, this locality is
with respect to time. In our formulation, it means that the
distribution over
![]() depends only on information
obtained at the current stage. In other settings, Markovian could
mean a dependency on a small number of stages, or even a local
dependency in terms of spatial relationships, as in a Markov
random field [231,377].
depends only on information
obtained at the current stage. In other settings, Markovian could
mean a dependency on a small number of stages, or even a local
dependency in terms of spatial relationships, as in a Markov
random field [231,377].
To make the Markov assumption more precise, the state and action histories as defined in Section 8.2.1 will be used again here. Let
| (10.1) |
| (10.2) |
| (10.3) |
The effect of nature is defined in the state transition equation,
which produces a new state, ![]() , once
, once ![]() ,
, ![]() , and
, and
![]() are given:
are given:
In the probabilistic case, a probability distribution over ![]() can be
derived for stage
can be
derived for stage ![]() , under the application of
, under the application of ![]() from
from ![]() .
As part of the problem,
.
As part of the problem,
![]() is given. Using the
state transition equation,
is given. Using the
state transition equation,
![]() ,
,
| (10.7) |
Putting these parts of the model together and adding some of the components from Formulation 2.3, leads to the following formulation:
Using Formulation 10.1, either a feasible or optimal
planning problem can be defined. To obtain a feasible planning
problem, let
![]() for all
for all ![]() ,
, ![]() , and
, and
![]() . Furthermore, let
. Furthermore, let
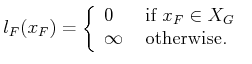 |
(10.9) |
Note that in each stage, the cost term is generally allowed to depend
on the nature action ![]() . If probabilistic uncertainty is
used, then Formulation 10.1 is often referred to as a
controlled Markov process or Markov decision process
(MDP). If the actions are removed from the formulation, then it is
simply referred to as a Markov process. In most statistical
literature, the name Markov chain is used instead of Markov
process when there are discrete stages (as opposed to continuous-time
Markov processes). Thus, the terms controlled Markov chain and
Markov decision chain may be preferable.
. If probabilistic uncertainty is
used, then Formulation 10.1 is often referred to as a
controlled Markov process or Markov decision process
(MDP). If the actions are removed from the formulation, then it is
simply referred to as a Markov process. In most statistical
literature, the name Markov chain is used instead of Markov
process when there are discrete stages (as opposed to continuous-time
Markov processes). Thus, the terms controlled Markov chain and
Markov decision chain may be preferable.
In some applications, it may be convenient to avoid the explicit
characterization of nature. Suppose that
![]() . If nondeterministic uncertainty is used, then
. If nondeterministic uncertainty is used, then
![]() can be specified for all
can be specified for all ![]() and
and
![]() as a substitute for the state transition equation; this avoids
having to refer to nature. The application of an action
as a substitute for the state transition equation; this avoids
having to refer to nature. The application of an action ![]() from a
state
from a
state ![]() directly leads to a specified subset of
directly leads to a specified subset of ![]() . If
probabilistic uncertainty is used, then
. If
probabilistic uncertainty is used, then
![]() can be
directly defined as the alternative to the state transition equation.
This yields a probability distribution over
can be
directly defined as the alternative to the state transition equation.
This yields a probability distribution over ![]() , if
, if ![]() is applied
from some
is applied
from some ![]() , once again avoiding explicit reference to nature.
Most of the time we will use a state transition equation that refers
to nature; however, it is important to keep these alternatives in
mind. They arise in many related books and research articles.
, once again avoiding explicit reference to nature.
Most of the time we will use a state transition equation that refers
to nature; however, it is important to keep these alternatives in
mind. They arise in many related books and research articles.
As used throughout Chapter 2, a directed state
transition graph is sometimes convenient for expressing the planning
problem. The same idea can be applied in the current setting. As in
Section 2.1, ![]() is the vertex set; however, the edge
definition must change to reflect nature. A directed edge exists from
state
is the vertex set; however, the edge
definition must change to reflect nature. A directed edge exists from
state ![]() to
to ![]() if there exists some
if there exists some
![]() and
and
![]() such that
such that
![]() . A weighted
graph can be made by associating the cost term
. A weighted
graph can be made by associating the cost term
![]() with each edge. In the case of a probabilistic model, the probability
of the transition occurring may also be associated with each edge.
with each edge. In the case of a probabilistic model, the probability
of the transition occurring may also be associated with each edge.
Note that both the decision maker and nature are needed to determine
which vertex will be reached. As the decision maker contemplates
applying an action ![]() from the state
from the state ![]() , it sees that there may be
several outgoing edges due to nature. If a different action is
contemplated, then this set of possible outgoing edges changes. Once
nature applies its action, then the particular edge is traversed to
arrive at the new state; however, this is not completely controlled by
the decision maker.
, it sees that there may be
several outgoing edges due to nature. If a different action is
contemplated, then this set of possible outgoing edges changes. Once
nature applies its action, then the particular edge is traversed to
arrive at the new state; however, this is not completely controlled by
the decision maker.
Consider executing a sequence of actions,
![]() , under
the nondeterministic uncertainty model. This means that we attempt to
move left two units in each stage. After the first
, under
the nondeterministic uncertainty model. This means that we attempt to
move left two units in each stage. After the first ![]() is applied,
the set of possible next states is
is applied,
the set of possible next states is
![]() . Nature may slow
down the progress to be only one unit per stage, or it may speed up
the progress so that
. Nature may slow
down the progress to be only one unit per stage, or it may speed up
the progress so that ![]() is three units closer per stage. Note
that after
is three units closer per stage. Note
that after ![]() stages, the goal is guaranteed to be achieved, in
spite of any possible actions of nature. Once
stages, the goal is guaranteed to be achieved, in
spite of any possible actions of nature. Once ![]() is reached,
is reached,
![]() should be applied. If the problem is changed so that
should be applied. If the problem is changed so that
![]() , it becomes impossible to guarantee that the goal will be
reached because nature may cause the goal to be overshot.
, it becomes impossible to guarantee that the goal will be
reached because nature may cause the goal to be overshot.
Now let
![]() and
and
![]() . Under
nondeterministic uncertainty, the problem can no longer be solved
because nature is now powerful enough to move the state completely in
the wrong direction in the worst case. A reasonable probabilistic
version of the problem can, however, be defined and solved. Suppose
that
. Under
nondeterministic uncertainty, the problem can no longer be solved
because nature is now powerful enough to move the state completely in
the wrong direction in the worst case. A reasonable probabilistic
version of the problem can, however, be defined and solved. Suppose
that
![]() for each
for each
![]() . The transition
probabilities can be defined from
. The transition
probabilities can be defined from ![]() . For example, if
. For example, if ![]() and
and ![]() , then
, then
![]() if
if
![]() , and
, and
![]() otherwise. With the
probabilistic formulation, there is a nonzero probability that the
goal,
otherwise. With the
probabilistic formulation, there is a nonzero probability that the
goal,
![]() , will be reached, even though in the
worst-case reaching the goal is not guaranteed.
, will be reached, even though in the
worst-case reaching the goal is not guaranteed.
![]()
Let
![]() be a set of actions, which denote ``stay,''
``right,'' ``up,'' ``left,'' and ``down,'' respectively. Let
be a set of actions, which denote ``stay,''
``right,'' ``up,'' ``left,'' and ``down,'' respectively. Let
![]() . For each
. For each ![]() , let
, let ![]() contain
contain ![]() and whichever
actions are applicable from
and whichever
actions are applicable from ![]() (some are not applicable along the
boundaries).
(some are not applicable along the
boundaries).
Let
![]() represent the set of all actions in
represent the set of all actions in ![]() that are
applicable after performing the move implied by
that are
applicable after performing the move implied by ![]() . For example, if
. For example, if
![]() and
and ![]() , then the robot is attempting to move to
, then the robot is attempting to move to
![]() . From this state, there are three neighboring states, each of
which corresponds to an action of nature. Thus,
. From this state, there are three neighboring states, each of
which corresponds to an action of nature. Thus,
![]() in this
case is
in this
case is
![]() . The action
. The action
![]() does not appear
because there is no state to the left of
does not appear
because there is no state to the left of ![]() . Suppose that the
probabilistic model is used, and that every nature action is equally
likely.
. Suppose that the
probabilistic model is used, and that every nature action is equally
likely.
The state transition function ![]() is formed by adding the effect of
both
is formed by adding the effect of
both ![]() and
and ![]() . For example, if
. For example, if
![]() ,
, ![]() ,
and
,
and
![]() , then
, then
![]() . If
. If ![]() had
been
had
been ![]() , then the two actions would cancel and
, then the two actions would cancel and
![]() .
Without nature, it would have been assumed that
.
Without nature, it would have been assumed that
![]() . As
always, the state never changes once
. As
always, the state never changes once ![]() is applied, regardless of
nature's actions.
is applied, regardless of
nature's actions.
For the cost functional, let
![]() (unless
(unless ![]() ; in this case,
; in this case,
![]() ). For the final stage, let
). For the final stage, let
![]() if
if
![]() ; otherwise, let
; otherwise, let
![]() . A reasonable task is to get the robot to terminate in
. A reasonable task is to get the robot to terminate in
![]() in the minimum expected number of stages. A feedback plan is
needed, which will be introduced in Section 10.1.3, and the
optimal plan for this problem can be efficiently computed using the
methods of Section 10.2.1.
in the minimum expected number of stages. A feedback plan is
needed, which will be introduced in Section 10.1.3, and the
optimal plan for this problem can be efficiently computed using the
methods of Section 10.2.1.
This example can be easily generalized to moving through a complicated
labyrinth in two or more dimensions. If the grid resolution is high,
then an approximation to motion planning is obtained. Rather than
forcing motions in only four directions, it may be preferable to allow
any direction. This case is covered in Section 10.6,
which addresses planning in continuous state spaces.
![]()
Steven M LaValle 2020-08-14