It is difficult to even define optimality for more general C-spaces.
What does it mean to have a shortest path in 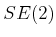 or
or 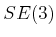 ?
Consider the case of a planar, rigid robot that can translate and
rotate. One path could minimize the amount of rotation whereas
another tries to minimize the amount of translation. Without more
information, there is no clear preference. Ulam's distance is one
possibility, which is to minimize the distance traveled by
?
Consider the case of a planar, rigid robot that can translate and
rotate. One path could minimize the amount of rotation whereas
another tries to minimize the amount of translation. Without more
information, there is no clear preference. Ulam's distance is one
possibility, which is to minimize the distance traveled by  fixed
points [474]. In Chapter 13, differential
models will be introduced, which lead to meaningful definitions of
optimality. For example, the shortest paths for a slow-moving car are
shown in Section 15.3; these require a precise
specification of the constraints on the motion of the car (it is more
costly to move a car sideways than forward).
fixed
points [474]. In Chapter 13, differential
models will be introduced, which lead to meaningful definitions of
optimality. For example, the shortest paths for a slow-moving car are
shown in Section 15.3; these require a precise
specification of the constraints on the motion of the car (it is more
costly to move a car sideways than forward).
This section formulates some optimal motion planning problems, to
provide a smooth transition into the later concepts. Up until now,
actions were used in Chapter 2 for discrete planning
problems, but they were successfully avoided for basic motion planning
by directly describing paths that map into
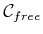 . It will be
convenient to use them once again. Recall that they were convenient
for defining costs and optimal planning in Section 2.3.
. It will be
convenient to use them once again. Recall that they were convenient
for defining costs and optimal planning in Section 2.3.
To avoid for now the complications of differential equations, consider
making an approximate model of motion planning in which every path
must be composed of a sequence of shortest-path segments in
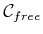 .
Most often these are line segments; however, for the case of
.
Most often these are line segments; however, for the case of 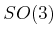 ,
circular arcs obtained by spherical linear interpolation may be
preferable. Consider extending Formulation 2.3 from Section
2.3.2 to the problem of motion planning.
,
circular arcs obtained by spherical linear interpolation may be
preferable. Consider extending Formulation 2.3 from Section
2.3.2 to the problem of motion planning.
Let the C-space  be embedded in
be embedded in
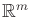 (i.e.,
(i.e.,
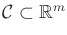 ). An action will be defined shortly as an
). An action will be defined shortly as an 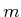 -dimensional
vector. Given a scaling constant
-dimensional
vector. Given a scaling constant 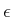 and a configuration
and a configuration 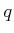 ,
an action
,
an action 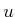 produces a new configuration,
produces a new configuration,
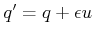 . This can be considered as a configuration transition
equation,
. This can be considered as a configuration transition
equation,
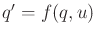 . The path segment represented by the
action
. The path segment represented by the
action 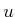 is the shortest path (usually a line segment) between
is the shortest path (usually a line segment) between 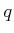 and
and 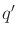 . Following Section 2.3, let
. Following Section 2.3, let 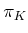 denote a
denote a 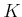 -step plan, which is a sequence
-step plan, which is a sequence 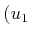 ,
, 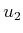 ,
,
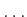 ,
, 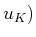 of
of 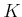 actions. Note that if
actions. Note that if 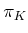 and
and 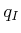 are given, then a sequence of states,
are given, then a sequence of states, 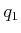 ,
, 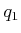 ,
, 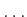 ,
,
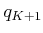 , can be derived using
, can be derived using 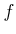 . Initially,
. Initially,
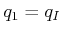 , and
each following state is obtained by
, and
each following state is obtained by
 . From this
a path,
. From this
a path,
![$ \tau: [0,1] \rightarrow {\cal C}$](img1939.gif) , can be derived.
, can be derived.
An approximate optimal planning problem is formalized as follows:
Formulation 7..4 (Approximate Optimal Motion Planning)
- The following components are defined the same as in Formulation
4.1:
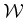 ,
, 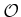 ,
, 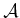 ,
,  ,
,
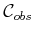 ,
,
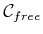 , and
, and
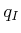 . It is assumed that
. It is assumed that  is an
is an  -dimensional manifold.
-dimensional manifold.
- For each
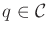 , a possibly infinite action space,
, a possibly infinite action space,
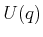 . Each
. Each 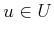 is an
is an  -dimensional vector.
-dimensional vector.
- A positive constant
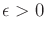 called the step size.
called the step size.
- A set of stages, each denoted by
 , which begins at
, which begins at
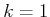 and continues indefinitely. Each stage is indicated by a
subscript, to obtain
and continues indefinitely. Each stage is indicated by a
subscript, to obtain 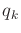 and
and 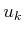 .
.
- A configuration transition function
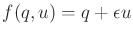 in which
in which
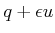 is computed by vector addition on
is computed by vector addition on
 .
.
- Instead of a goal state, a goal region
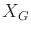 is defined.
is defined.
- Let
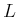 denote a real-valued cost functional, which is
applied to a
denote a real-valued cost functional, which is
applied to a 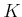 -step plan,
-step plan, 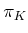 . This means that the sequence
. This means that the sequence
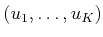 of actions and the sequence
of actions and the sequence
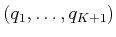 of configurations may appear in an expression of
of configurations may appear in an expression of  . Let
. Let 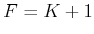 .
The cost functional is
.
The cost functional is
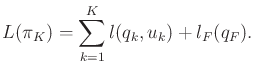 |
(7.26) |
The final term 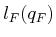 is outside of the sum and is defined as
is outside of the sum and is defined as
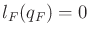 if
if
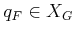 and
and
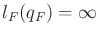 otherwise.
As in Formulation 2.3,
otherwise.
As in Formulation 2.3, 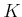 is not necessarily a constant.
is not necessarily a constant.
- Each
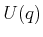 contains the special termination action
contains the special termination action 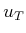 ,
which behaves the same way as in Formulation 2.3. If
,
which behaves the same way as in Formulation 2.3. If 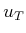 is applied to
is applied to 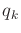 at stage
at stage  , then the action is repeatedly
applied forever, the configuration remains in
, then the action is repeatedly
applied forever, the configuration remains in 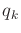 forever, and no
more cost accumulates.
forever, and no
more cost accumulates.
The task is to compute a sequence of actions that optimizes
(7.26). Formulation 7.4 can be used to define
a variety of optimal planning problems. The parameter 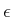 can
be considered as the resolution of the approximation. In many
formulations it can be interpreted as a time step,
can
be considered as the resolution of the approximation. In many
formulations it can be interpreted as a time step,
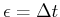 ; however, note that no explicit time reference is necessary
because the problem only requires constructing a path through
; however, note that no explicit time reference is necessary
because the problem only requires constructing a path through
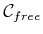 .
As
.
As 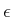 approaches zero, the formulation approaches an exact
optimal planning problem. To properly express the exact problem,
differential equations are needed. This is deferred until Part
IV.
approaches zero, the formulation approaches an exact
optimal planning problem. To properly express the exact problem,
differential equations are needed. This is deferred until Part
IV.
Figure 7.40:
Under the Manhattan (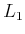 ) motion
model, all monotonic paths that follow the grid directions have
equivalent length.
) motion
model, all monotonic paths that follow the grid directions have
equivalent length.
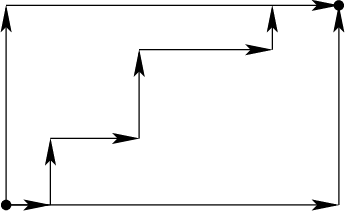 |
Figure 7.41:
Depictions of the action sets, 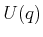 , for
Examples 7.4, 7.5, and
7.6.
, for
Examples 7.4, 7.5, and
7.6.
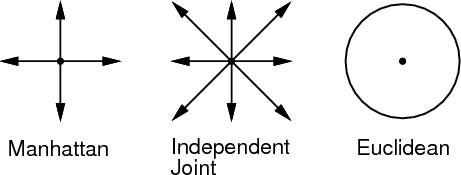 |
Example 7..4 (Manhattan Motion Model)
Suppose that in addition to
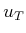
, the action set
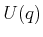
contains
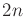
vectors in which only one component is nonzero and must take the value
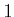
or
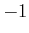
. For example, if
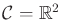
, then
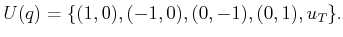 |
(7.27) |
When used in the configuration transition equation, this set of
actions produces ``up,'' ``down,'' ``left,'' and ``right'' motions and
a ``terminate'' command. This produces a topological graph according
to the 1-neighborhood model, (
5.37), which was given in
Section
5.4.2. The action set for this example and the
following two examples are shown in Figure
7.41 for
comparison. The cost term
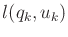
is defined to be
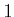
for all
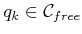
and
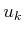
. If
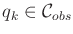
, then
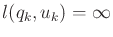
. Note that the set of configurations reachable by these
actions lies on a grid, in which the spacing between
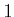
-neighbors is
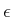
. This corresponds to a convenient special case in which
time discretization (implemented by
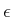
) leads to a regular
space discretization. Consider Figure
7.40. It is
impossible to take a shorter path along a diagonal because the actions
do not allow it. Therefore, all monotonic paths along the grid
produce the same costs.
Optimal paths can be obtained by simply applying the dynamic
programming algorithms of Chapter 2. This example
provides a nice unification of concepts from Section 2.2,
which introduced grid search, and Section 5.4.2, which
explained how to adapt search methods to motion planning. In the
current setting, only algorithms that produce optimal solutions on the
corresponding graph are acceptable.
This form of optimization might not seem relevant because it does not
represent the Euclidean shortest-path problem for
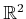 . The next
model adds more actions, and does correspond to an important class of
optimization problems in robotics.
. The next
model adds more actions, and does correspond to an important class of
optimization problems in robotics.

Example 7..5 (Independent-Joint Motion Model)
Now suppose that
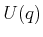
includes
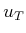
and the set of all
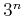
vectors for which every
element is either
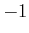
,
0, or
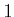
. Under this model, a path can be
taken along any diagonal. This still does not change the fact that
all reachable configurations lie on a grid. Therefore, the standard
grid algorithms can be applied once again. The difference is that now
there are
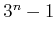
edges emanating from every vertex, as opposed to
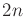
in Example
7.4. This model is appropriate for
robots that are constructed from a collection of links attached by
revolute joints. If each joint is operated independently, then it
makes sense that each joint could be moved either forward, backward,
or held stationary. This corresponds exactly to the actions.
However, this model cannot nicely approximate Euclidean shortest
paths; this motivates the next example.

Example 7..6 (Euclidean Motion Model)
To approximate Euclidean shortest
paths, let
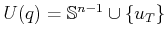
, in which
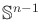
is the
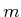
-dimensional unit sphere centered at the origin of
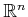
. This
means that in

stages, any piecewise-linear path in which each
segment has length
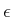
can be formed by a sequence of inputs.
Therefore, the set of reachable states is no longer confined to a
grid. Consider taking
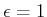
, and pick any point, such as
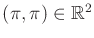
. How close can you come to this point? It
turns out that the set of points reachable with this model is dense in
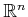
if obstacles are neglected. This means that we can come
arbitrarily close to any point in
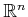
. Therefore, a finite grid
cannot be used to represent the problem. Approximate solutions can
still be obtained by numerically computing an optimal cost-to-go
function over

. This approach is presented in Section
8.5.2.
One additional issue for this problem is the precision defined for the
goal. If the goal region is very small relative to 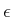 , then
complicated paths may have to be selected to arrive precisely at the
goal.
, then
complicated paths may have to be selected to arrive precisely at the
goal.

Example 7..7 (Weighted-Region Problem)
In outdoor and planetary
navigation applications, it does not make sense to define obstacles in
the crisp way that has been used so far. For each patch of terrain,
it is more convenient to associate a cost that indicates the estimated
difficulty of its traversal. This is sometimes considered as a
``grayscale'' model of obstacles. The model can be easily captured in
the cost term
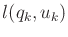
. The action spaces can be borrowed from
Examples
7.4 or
7.5. Stentz's
algorithm
[
913], which is introduced in Section
12.3.2, generates optimal navigation plans for this problem,
even assuming that the terrain is initially unknown. Theoretical
bounds for optimal weighted-region planning problems are given in
[
709,
710]. An approximation algorithm appears in
[
820].

Steven M LaValle
2020-08-14

![]() or
or ![]() ?
Consider the case of a planar, rigid robot that can translate and
rotate. One path could minimize the amount of rotation whereas
another tries to minimize the amount of translation. Without more
information, there is no clear preference. Ulam's distance is one
possibility, which is to minimize the distance traveled by
?
Consider the case of a planar, rigid robot that can translate and
rotate. One path could minimize the amount of rotation whereas
another tries to minimize the amount of translation. Without more
information, there is no clear preference. Ulam's distance is one
possibility, which is to minimize the distance traveled by ![]() fixed
points [474]. In Chapter 13, differential
models will be introduced, which lead to meaningful definitions of
optimality. For example, the shortest paths for a slow-moving car are
shown in Section 15.3; these require a precise
specification of the constraints on the motion of the car (it is more
costly to move a car sideways than forward).
fixed
points [474]. In Chapter 13, differential
models will be introduced, which lead to meaningful definitions of
optimality. For example, the shortest paths for a slow-moving car are
shown in Section 15.3; these require a precise
specification of the constraints on the motion of the car (it is more
costly to move a car sideways than forward).
![]() . It will be
convenient to use them once again. Recall that they were convenient
for defining costs and optimal planning in Section 2.3.
. It will be
convenient to use them once again. Recall that they were convenient
for defining costs and optimal planning in Section 2.3.
![]() .
Most often these are line segments; however, for the case of
.
Most often these are line segments; however, for the case of ![]() ,
circular arcs obtained by spherical linear interpolation may be
preferable. Consider extending Formulation 2.3 from Section
2.3.2 to the problem of motion planning.
,
circular arcs obtained by spherical linear interpolation may be
preferable. Consider extending Formulation 2.3 from Section
2.3.2 to the problem of motion planning.
![]() be embedded in
be embedded in
![]() (i.e.,
(i.e.,
![]() ). An action will be defined shortly as an
). An action will be defined shortly as an ![]() -dimensional
vector. Given a scaling constant
-dimensional
vector. Given a scaling constant ![]() and a configuration
and a configuration ![]() ,
an action
,
an action ![]() produces a new configuration,
produces a new configuration,
![]() . This can be considered as a configuration transition
equation,
. This can be considered as a configuration transition
equation,
![]() . The path segment represented by the
action
. The path segment represented by the
action ![]() is the shortest path (usually a line segment) between
is the shortest path (usually a line segment) between ![]() and
and ![]() . Following Section 2.3, let
. Following Section 2.3, let ![]() denote a
denote a ![]() -step plan, which is a sequence
-step plan, which is a sequence ![]() ,
, ![]() ,
,
![]() ,
, ![]() of
of ![]() actions. Note that if
actions. Note that if ![]() and
and ![]() are given, then a sequence of states,
are given, then a sequence of states, ![]() ,
, ![]() ,
, ![]() ,
,
![]() , can be derived using
, can be derived using ![]() . Initially,
. Initially,
![]() , and
each following state is obtained by
, and
each following state is obtained by
![]() . From this
a path,
. From this
a path,
![]() , can be derived.
, can be derived.
![]() can
be considered as the resolution of the approximation. In many
formulations it can be interpreted as a time step,
can
be considered as the resolution of the approximation. In many
formulations it can be interpreted as a time step,
![]() ; however, note that no explicit time reference is necessary
because the problem only requires constructing a path through
; however, note that no explicit time reference is necessary
because the problem only requires constructing a path through
![]() .
As
.
As ![]() approaches zero, the formulation approaches an exact
optimal planning problem. To properly express the exact problem,
differential equations are needed. This is deferred until Part
IV.
approaches zero, the formulation approaches an exact
optimal planning problem. To properly express the exact problem,
differential equations are needed. This is deferred until Part
IV.

![]() . The next
model adds more actions, and does correspond to an important class of
optimization problems in robotics.
. The next
model adds more actions, and does correspond to an important class of
optimization problems in robotics.
![]()
![]() , then
complicated paths may have to be selected to arrive precisely at the
goal.
, then
complicated paths may have to be selected to arrive precisely at the
goal.
![]()