For each grid point 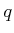 we need to define the set of nearby grid
points for which an edge may be constructed. Special care must be
given to defining the neighborhood of a boundary grid point to ensure
that identifications and the C-space boundary (if it exists) are
respected. If
we need to define the set of nearby grid
points for which an edge may be constructed. Special care must be
given to defining the neighborhood of a boundary grid point to ensure
that identifications and the C-space boundary (if it exists) are
respected. If 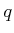 is not a boundary grid point, then the
1-neighborhood is defined as
is not a boundary grid point, then the
1-neighborhood is defined as
 |
(5.37) |
For an 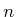 -dimensional C-space there at most
-dimensional C-space there at most 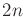
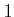 -neighbors. In
two dimensions, this yields at most four
-neighbors. In
two dimensions, this yields at most four 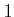 -neighbors, which can be
thought of as ``up,'' ``down,'' ``left,'' and ``right.'' There are
at most four because some directions may be blocked by the
obstacle region.
-neighbors, which can be
thought of as ``up,'' ``down,'' ``left,'' and ``right.'' There are
at most four because some directions may be blocked by the
obstacle region.
A 2-neighborhood is defined as
 |
(5.38) |
Similarly, a 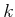 -neighborhood can be defined for any positive
integer
-neighborhood can be defined for any positive
integer  . For an
. For an 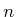 -neighborhood, there are at most
-neighborhood, there are at most 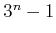 neighbors; there may be fewer due to boundaries or collisions. The
definitions can be easily extended to handle the boundary points.
neighbors; there may be fewer due to boundaries or collisions. The
definitions can be easily extended to handle the boundary points.
Figure 5.14:
A topological graph can be constructed
during the search and can successfully solve a motion planning
problem using very few samples.
 |
Steven M LaValle
2020-08-14

![]() we need to define the set of nearby grid
points for which an edge may be constructed. Special care must be
given to defining the neighborhood of a boundary grid point to ensure
that identifications and the C-space boundary (if it exists) are
respected. If
we need to define the set of nearby grid
points for which an edge may be constructed. Special care must be
given to defining the neighborhood of a boundary grid point to ensure
that identifications and the C-space boundary (if it exists) are
respected. If ![]() is not a boundary grid point, then the
1-neighborhood is defined as
is not a boundary grid point, then the
1-neighborhood is defined as
