- Extend the vertical decomposition algorithm to correctly handle
the case in which
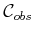 has two or more points that lie on the same
vertical line. This includes the case of vertical segments. Random
perturbations are not allowed.
has two or more points that lie on the same
vertical line. This includes the case of vertical segments. Random
perturbations are not allowed.
- Fully describe and prove the correctness of the bitangent
computation method shown in Figure 6.14, which
avoids trigonometric functions. Make certain that all types of
bitangents (in general position) are considered.
- Develop an algorithm that uses the plane-sweep principle to
efficiently compute a representation of the union of two nonconvex
polygons.
- Extend the vertical cell decomposition algorithm of Section
6.2.2 to work for obstacle boundaries that are described as
chains of circular arcs and line segments.
- Extend the shortest-path roadmap algorithm of Section
6.2.4 to work for obstacle boundaries that are described
as chains of circular arcs and line segments.
- Derive the equation for the Conchoid of Nicomedes, shown in
Figure 6.24, for the case of a line-segment robot
contacting an obstacle vertex and edge simultaneously.
- Propose a resolution-complete algorithm for
motion planning of the line-segment robot in a polygonal obstacle
region. The algorithm should compute exact C-space obstacle slices
for any fixed orientation,
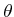 ; however, the algorithm should use
van der Corput sampling over the set
; however, the algorithm should use
van der Corput sampling over the set 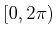 of orientations.
of orientations.
- Determine the result of cylindrical algebraic decomposition for
unit spheres
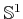 ,
,
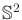 ,
,
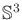 ,
,
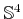 ,
, 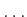 . Each
. Each
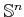 is expressed as a unit sphere in
is expressed as a unit sphere in
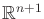 . Graphically depict the
cases of
. Graphically depict the
cases of
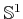 and
and
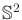 . Also, attempt to develop an expression
for the number of cells as a function of
. Also, attempt to develop an expression
for the number of cells as a function of  .
.
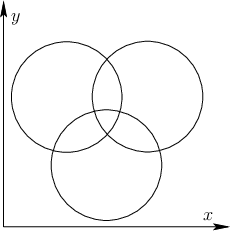
- Determine the cylindrical algebraic decomposition for the three
intersecting circles shown in Figure 6.43. How many
cells are obtained?
- Using the matrix in (6.28), show that the result of
Canny's roadmap for the torus, shown in Figure 6.39, is
correct. Use the torus equation
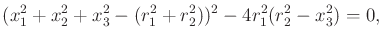 |
(6.40) |
in which 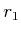 is the major circle,
is the major circle, 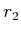 is the minor circle, and
is the minor circle, and
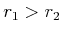 .
.
Figure 6.43:
Determine the cylindrical algebraic
decomposition obtained by projecting onto the 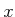 -axis.
-axis.
 |
- Propose a vertical decomposition algorithm for a polygonal robot
that can translate in the plane and even continuously vary its scale.
How would the algorithm be modified to instead work for a robot that
can translate or be sheared?
- Develop a shortest-path roadmap algorithm for a flat torus,
defined by identifying opposite edges of a square. Use Euclidean
distance but respect the identifications when determining the
shortest path. Assume the robot is a point and the obstacles are
polygonal.
Implementations
- Implement the vertical cell decomposition planning algorithm of
Section 6.2.2.
- Implement the maximum-clearance roadmap planning algorithm of Section
6.2.3.
- Implement a planning algorithm for a point robot that moves in
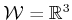 among polyhedral obstacles. Use vertical decomposition.
among polyhedral obstacles. Use vertical decomposition.
- Implement an algorithm that performs a cylindrical decomposition
of a polygonal obstacle region.
- Implement an algorithm that computes the cell decomposition of
Section 6.3.4 for the line-segment robot.
- Experiment with cylindrical algebraic decomposition. The
project can be greatly facilitated by utilizing existing packages for
performing basic operations in computational algebraic geometry.
- Implement the algorithm proposed in Exercise 7.
Steven M LaValle
2020-08-14
