Virtually all combinatorial motion planning approaches construct a
roadmap along the way to solving queries. This notion was
introduced in Section 5.6, but in this chapter
stricter requirements are imposed in the roadmap definition because
any algorithm that constructs one needs to be complete. Some of the
algorithms in this chapter first construct a cell decomposition of
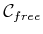 from which the roadmap is consequently derived. Other
methods directly construct a roadmap without the consideration of
cells.
from which the roadmap is consequently derived. Other
methods directly construct a roadmap without the consideration of
cells.
Let 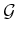 be a topological graph (defined in Example
4.6) that maps into
be a topological graph (defined in Example
4.6) that maps into
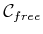 . Furthermore, let
. Furthermore, let
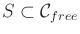 be the swath, which is set of all points reached by
be the swath, which is set of all points reached by
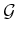 , as defined in (5.40). The graph
, as defined in (5.40). The graph 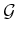 is called
a roadmap if it satisfies two important conditions:
is called
a roadmap if it satisfies two important conditions:
- Accessibility: From
any
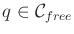 , it is simple and efficient to compute a path
, it is simple and efficient to compute a path
![$ \tau: [0,1] \rightarrow {\cal C}_{free}$](img1368.gif) such that
such that
 and
and
 ,
in which
,
in which 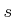 may be any point in
may be any point in 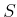 . Usually,
. Usually, 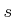 is the closest
point to
is the closest
point to 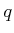 , assuming
, assuming 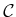 is a metric space.
is a metric space.
- Connectivity-preserving:
Using the first condition, it is always possible to connect some
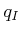 and
and 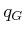 to some
to some 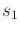 and
and 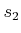 , respectively, in
, respectively, in 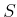 .
The second condition requires that if there exists a path
.
The second condition requires that if there exists a path
![$ \tau: [0,1] \rightarrow {\cal C}_{free}$](img1368.gif) such that
such that
 and
and
 , then there also exists a path
, then there also exists a path
![$ \tau^\prime: [0,1] \rightarrow
S$](img2108.gif) , such that
, such that
 and
and
 .
Thus, solutions are not missed because
.
Thus, solutions are not missed because 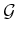 fails to capture the
connectivity of
fails to capture the
connectivity of
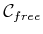 . This ensures that complete algorithms are
developed.
. This ensures that complete algorithms are
developed.
By satisfying these properties, a roadmap provides a discrete
representation of the continuous motion planning problem without
losing any of the original connectivity information needed to solve
it. A query,
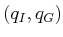 , is solved by connecting each query
point to the roadmap and then performing a discrete graph search on
, is solved by connecting each query
point to the roadmap and then performing a discrete graph search on
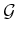 . To maintain completeness, the first condition ensures that
any query can be connected to
. To maintain completeness, the first condition ensures that
any query can be connected to 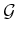 , and the second condition
ensures that the search always succeeds if a solution exists.
, and the second condition
ensures that the search always succeeds if a solution exists.
Steven M LaValle
2020-08-14

![]() from which the roadmap is consequently derived. Other
methods directly construct a roadmap without the consideration of
cells.
from which the roadmap is consequently derived. Other
methods directly construct a roadmap without the consideration of
cells.
![]() be a topological graph (defined in Example
4.6) that maps into
be a topological graph (defined in Example
4.6) that maps into
![]() . Furthermore, let
. Furthermore, let
![]() be the swath, which is set of all points reached by
be the swath, which is set of all points reached by
![]() , as defined in (5.40). The graph
, as defined in (5.40). The graph ![]() is called
a roadmap if it satisfies two important conditions:
is called
a roadmap if it satisfies two important conditions: