
Next: 5.5.2 Efficiently Finding Nearest Up: 5.5 Rapidly Exploring Dense Previous: 5.5 Rapidly Exploring Dense
Before explaining how to use these trees to solve a planning query,
imagine that the goal is to get as close as possible to every
configuration, starting from an initial configuration. The method
works for any dense sequence. Once again, let ![]() denote an
infinite, dense sequence of samples in
denote an
infinite, dense sequence of samples in ![]() . The
. The ![]() th sample is
denoted by
th sample is
denoted by
![]() . This may possibly include a uniform, random
sequence, which is only dense with probability one. Random sequences
that induce a nonuniform bias are also acceptable, as long as they are
dense with probability one.
. This may possibly include a uniform, random
sequence, which is only dense with probability one. Random sequences
that induce a nonuniform bias are also acceptable, as long as they are
dense with probability one.
An RDT is a topological graph,
![]() . Let
. Let
![]() indicate the set of all points reached by
indicate the set of all points reached by ![]() . Since each
. Since each ![]() is a path, this can be expressed as the swath,
is a path, this can be expressed as the swath, ![]() , of the
graph, which is defined as
, of the
graph, which is defined as
 |
 |
![\includegraphics[width=3.5truein]{figs/rdt3.eps}](img2042.gif) |
 |
The exploration algorithm is first explained in Figure
5.16 without any obstacles or boundary obstructions. It
is assumed that ![]() is a metric space. Initially, a vertex is made
at
is a metric space. Initially, a vertex is made
at ![]() . For
. For ![]() iterations, a tree is iteratively grown by
connecting
iterations, a tree is iteratively grown by
connecting
![]() to its nearest point in the swath,
to its nearest point in the swath, ![]() .
The connection is usually made along the shortest possible path. In
every iteration,
.
The connection is usually made along the shortest possible path. In
every iteration,
![]() becomes a vertex. Therefore, the
resulting tree is dense. Figures 5.17-5.18
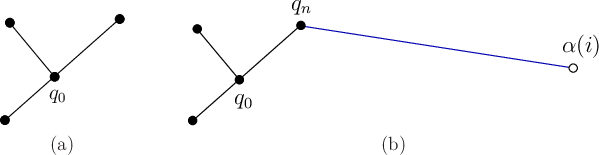
illustrate an iteration graphically. Suppose the tree has three edges
and four vertices, as shown in Figure 5.17a. If the nearest
point,
becomes a vertex. Therefore, the
resulting tree is dense. Figures 5.17-5.18
illustrate an iteration graphically. Suppose the tree has three edges
and four vertices, as shown in Figure 5.17a. If the nearest
point, ![]() , to
, to
![]() is a vertex, as shown in Figure
5.17b, then an edge is made from
is a vertex, as shown in Figure
5.17b, then an edge is made from ![]() to
to
![]() .
However, if the nearest point lies in the interior of an edge, as
shown in Figure 5.18, then the existing edge is split so
that
.
However, if the nearest point lies in the interior of an edge, as
shown in Figure 5.18, then the existing edge is split so
that ![]() appears as a new vertex, and an edge is made from
appears as a new vertex, and an edge is made from ![]() to
to
![]() . The edge splitting, if required, is assumed to be
handled in line 4 by the method that adds edges. Note that the total
number of edges may increase by one or two in each iteration.
. The edge splitting, if required, is assumed to be
handled in line 4 by the method that adds edges. Note that the total
number of edges may increase by one or two in each iteration.
The method as described here does not fit precisely under the general
framework from Section 5.4.1; however, with the
modifications suggested in Section 5.5.2, it can be
adapted to fit. In the RDT formulation, the NEAREST function
serves the purpose of the VSM, but in
the RDT, a point may be selected from anywhere in the swath of
the graph. The VSM can be generalized
to a swath-point selection method, SSM. This generalization
will be used in Section 14.3.4. The LPM tries to connect
![]() to
to ![]() along the
shortest path possible in
along the
shortest path possible in ![]() .
.
Figure 5.19 shows an execution of the algorithm in Figure
5.16 for the case in which
![]() and
and
![]() . It exhibits a kind of fractal behavior.5.15Several main branches are first constructed as it rapidly reaches the
far corners of the space. Gradually, more and more area is filled in
by smaller branches. From the pictures, it is clear that in the
limit, the tree densely fills the space. Thus, it can be seen that
the tree gradually improves the resolution (or dispersion) as the
iterations continue. This behavior turns out to be ideal for
sampling-based motion planning.
. It exhibits a kind of fractal behavior.5.15Several main branches are first constructed as it rapidly reaches the
far corners of the space. Gradually, more and more area is filled in
by smaller branches. From the pictures, it is clear that in the
limit, the tree densely fills the space. Thus, it can be seen that
the tree gradually improves the resolution (or dispersion) as the
iterations continue. This behavior turns out to be ideal for
sampling-based motion planning.
![\includegraphics[width=4.0truein]{figs/rdt5.eps}](img2047.gif) |
Recall that in sampling-based motion planning, the obstacle region
![]() is not explicitly represented. Therefore, it must be taken
into account in the construction of the tree. Figure 5.20
indicates how to modify the algorithm in Figure 5.16 so
that collision checking is taken into account. The modified algorithm
appears in Figure 5.21. The procedure STOPPING-CONFIGURATION yields the nearest configuration possible to
the boundary of
is not explicitly represented. Therefore, it must be taken
into account in the construction of the tree. Figure 5.20
indicates how to modify the algorithm in Figure 5.16 so
that collision checking is taken into account. The modified algorithm
appears in Figure 5.21. The procedure STOPPING-CONFIGURATION yields the nearest configuration possible to
the boundary of
![]() , along the direction toward
, along the direction toward ![]() . The
nearest point
. The
nearest point ![]() is defined to be same (obstacles are
ignored); however, the new edge might not reach to
is defined to be same (obstacles are
ignored); however, the new edge might not reach to
![]() . In
this case, an edge is made from
. In
this case, an edge is made from ![]() to
to ![]() , the last point
possible before hitting the obstacle. How close can the edge come to
the obstacle boundary? This depends on the method used to check for
collision, as explained in Section 5.3.4. It is
sometimes possible that
, the last point
possible before hitting the obstacle. How close can the edge come to
the obstacle boundary? This depends on the method used to check for
collision, as explained in Section 5.3.4. It is
sometimes possible that ![]() is already as close as possible to the
boundary of
is already as close as possible to the
boundary of
![]() in the direction of
in the direction of
![]() . In this case,
no new edge or vertex is added that for that iteration.
. In this case,
no new edge or vertex is added that for that iteration.
Steven M LaValle 2020-08-14