
Next: 5.4.2 Adapting Discrete Search Up: 5.4 Incremental Sampling and Previous: 5.4 Incremental Sampling and
The algorithms of Sections 5.4 and 5.5 follow
the single-query model, which means
![]() is given only once per robot and obstacle set. This
means that there are no advantages to precomputation, and the
sampling-based motion planning problem can be considered as a kind of
search. The multiple-query model, which favors precomputation,
is covered in Section 5.6.
is given only once per robot and obstacle set. This
means that there are no advantages to precomputation, and the
sampling-based motion planning problem can be considered as a kind of
search. The multiple-query model, which favors precomputation,
is covered in Section 5.6.
The sampling-based planning algorithms presented in the present
section are strikingly similar to the family of search algorithms
summarized in Section 2.2.4. The main difference
lies in step 3 below, in which applying an action, ![]() , is replaced by
generating a path segment,
, is replaced by
generating a path segment, ![]() . Another difference is that the
search graph,
. Another difference is that the
search graph, ![]() , is undirected, with edges that represent
paths, as opposed to a directed graph in which edges represent
actions. It is possible to make these look similar by defining an
action space for motion planning that consists of a collection of
paths, but this is avoided here. In the case of motion planning with
differential constraints, this will actually be required; see Chapter
14.
, is undirected, with edges that represent
paths, as opposed to a directed graph in which edges represent
actions. It is possible to make these look similar by defining an
action space for motion planning that consists of a collection of
paths, but this is avoided here. In the case of motion planning with
differential constraints, this will actually be required; see Chapter
14.
Most single-query, sampling-based planning algorithms follow this template:
In the present context, ![]() is a topological graph, as defined in
Example 4.6. Each vertex is a configuration and each
edge is a path that connects two configurations. In this chapter, it
will be simply referred to as a graph when there is no chance of
confusion. Some authors refer to such a graph as a roadmap;
however, we reserve the term roadmap for a graph that contains enough
paths to make any motion planning query easily solvable. This case is
covered in Section 5.6 and throughout Chapter
6.
is a topological graph, as defined in
Example 4.6. Each vertex is a configuration and each
edge is a path that connects two configurations. In this chapter, it
will be simply referred to as a graph when there is no chance of
confusion. Some authors refer to such a graph as a roadmap;
however, we reserve the term roadmap for a graph that contains enough
paths to make any motion planning query easily solvable. This case is
covered in Section 5.6 and throughout Chapter
6.
A large family of sampling-based algorithms can be described by
varying the implementations of steps 2 and 3. Implementations of the
other steps may also vary, but this is less important and will be
described where appropriate. For convenience, step 2 will be called
the vertex selection method (VSM) and
step 3 will be called the local planning method (LPM). The role of the VSM is similar to that of the
priority queue, ![]() , in Section 2.2.1. The role of the
LPM is to compute a collision-free path segment that can be added to
the graph. It is called local because the path segment is
usually simple (e.g., the shortest path) and travels a short distance.
It is not global in the sense that the LPM does not try to solve
the entire planning problem; it is expected that the LPM may often fail to construct path segments.
, in Section 2.2.1. The role of the
LPM is to compute a collision-free path segment that can be added to
the graph. It is called local because the path segment is
usually simple (e.g., the shortest path) and travels a short distance.
It is not global in the sense that the LPM does not try to solve
the entire planning problem; it is expected that the LPM may often fail to construct path segments.
 |
It will be formalized shortly, but imagine for the time being that any
of the search algorithms from Section 2.2 may be applied
to motion planning by approximating ![]() with a high-resolution grid.
The resulting problem looks like a multi-dimensional extension of
Example 2.1 (the ``labyrinth'' walls are formed by
with a high-resolution grid.
The resulting problem looks like a multi-dimensional extension of
Example 2.1 (the ``labyrinth'' walls are formed by
![]() ). For a high-resolution grid in a high-dimensional space,
most classical discrete searching algorithms have trouble getting
trapped in a local minimum. There could be an astronomical number of
configurations that fall within a concavity in
). For a high-resolution grid in a high-dimensional space,
most classical discrete searching algorithms have trouble getting
trapped in a local minimum. There could be an astronomical number of
configurations that fall within a concavity in
![]() that must be
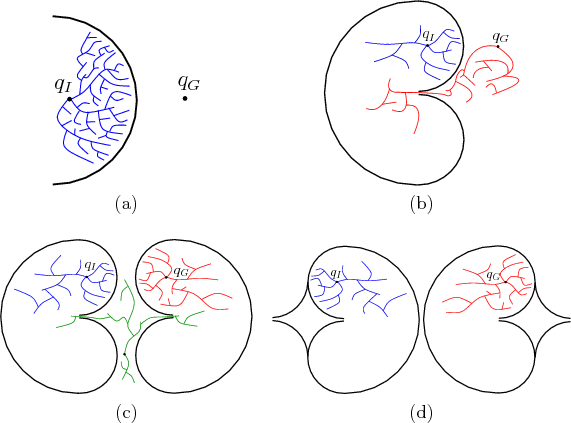
escaped to solve the problem, as shown in Figure 5.13a.
Imagine a problem in which the C-space obstacle is a giant ``bowl''
that can trap the configuration. This figure is drawn in two
dimensions, but imagine that the
that must be
escaped to solve the problem, as shown in Figure 5.13a.
Imagine a problem in which the C-space obstacle is a giant ``bowl''
that can trap the configuration. This figure is drawn in two
dimensions, but imagine that the ![]() has many dimensions, such as six
for
has many dimensions, such as six
for ![]() or perhaps dozens for a linkage. If the discrete planning
algorithms from Section 2.2 are applied to a
high-resolution grid approximation of
or perhaps dozens for a linkage. If the discrete planning
algorithms from Section 2.2 are applied to a
high-resolution grid approximation of ![]() , then they will all waste
their time filling up the bowl before being able to escape to
, then they will all waste
their time filling up the bowl before being able to escape to
![]() . The number of grid points in this bowl would typically be
on the order of
. The number of grid points in this bowl would typically be
on the order of ![]() for an
for an ![]() -dimensional C-space. Therefore,
sampling-based motion planning algorithms combine sampling and
searching in a way that attempts to overcome this difficulty.
-dimensional C-space. Therefore,
sampling-based motion planning algorithms combine sampling and
searching in a way that attempts to overcome this difficulty.
As in the case of discrete search algorithms, there are several classes of algorithms based on the number of search trees.
Of course, one can play the devil's advocate and construct the example in Figure 5.13d, for which virtually all sampling-based planning algorithms are doomed. Even harder versions can be made in which a sequence of several narrow corridors must be located and traversed. We must accept the fact that some problems are hopeless to solve using sampling-based planning methods, unless there is some problem-specific structure that can be additionally exploited.
Steven M LaValle 2020-08-14