Several possible implementations of line 5 can be made. In all of
these, it seems best to sort the vertices that will be considered for
connection in order of increasing distance from
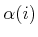 . This
makes sense because shorter paths are usually less costly to check for
collision, and they also have a higher likelihood of being
collision-free. If a connection is made, this avoids costly collision
checking of longer paths to configurations that would eventually
belong to the same connected component.
. This
makes sense because shorter paths are usually less costly to check for
collision, and they also have a higher likelihood of being
collision-free. If a connection is made, this avoids costly collision
checking of longer paths to configurations that would eventually
belong to the same connected component.
Several useful implementations of NEIGHBORHOOD are
- Nearest K: The
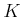 closest points to
closest points to
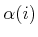 are
considered. This requires setting the parameter
are
considered. This requires setting the parameter 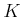 (a typical value
is
(a typical value
is 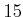 ). If you are unsure which implementation to use, try this
one.
). If you are unsure which implementation to use, try this
one.
- Component K: Try to obtain up to
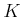 nearest samples from
each connected component of
nearest samples from
each connected component of 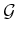 . A reasonable value is
. A reasonable value is  ;
otherwise, too many connections would be tried.
;
otherwise, too many connections would be tried.
- Radius: Take all points within a ball of radius
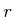 centered at
centered at
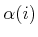 . An upper limit,
. An upper limit, 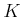 , may be set to prevent
too many connections from being attempted. Typically,
, may be set to prevent
too many connections from being attempted. Typically, 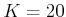 . A
radius can be determined adaptively by shrinking the ball as the
number of points increases. This reduction can be based on dispersion
or discrepancy, if either of these is available for
. A
radius can be determined adaptively by shrinking the ball as the
number of points increases. This reduction can be based on dispersion
or discrepancy, if either of these is available for 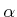 . Note
that if the samples are highly regular (e.g., a grid), then choosing
the nearest
. Note
that if the samples are highly regular (e.g., a grid), then choosing
the nearest 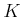 and taking points within a ball become essentially
equivalent. If the point set is highly irregular, as in the case of
random samples, then taking the nearest
and taking points within a ball become essentially
equivalent. If the point set is highly irregular, as in the case of
random samples, then taking the nearest 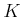 seems preferable.
seems preferable.
- Visibility: In Section 5.6.2, a variant
will be described for which it is worthwhile to try connecting
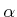 to all vertices in
to all vertices in 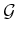 .
.
Note that all of these require 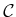 to be a metric space. One
variation that has not yet been given much attention is to ensure that
the directions of the NEIGHBORHOOD points relative to
to be a metric space. One
variation that has not yet been given much attention is to ensure that
the directions of the NEIGHBORHOOD points relative to
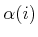 are distributed uniformly. For example, if the
are distributed uniformly. For example, if the 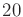 closest points are all clumped together in the same direction, then it
may be preferable to try connecting to a further point because it is
in the opposite direction.
closest points are all clumped together in the same direction, then it
may be preferable to try connecting to a further point because it is
in the opposite direction.
Steven M LaValle
2020-08-14

![]() . This
makes sense because shorter paths are usually less costly to check for
collision, and they also have a higher likelihood of being
collision-free. If a connection is made, this avoids costly collision
checking of longer paths to configurations that would eventually
belong to the same connected component.
. This
makes sense because shorter paths are usually less costly to check for
collision, and they also have a higher likelihood of being
collision-free. If a connection is made, this avoids costly collision
checking of longer paths to configurations that would eventually
belong to the same connected component.