
Next: Asymptotic bounds Up: 5.2 Sampling Theory Previous: Dispersion bounds
In some applications, selecting points that align with the coordinate
axis may be undesirable. Therefore, extensive sampling theory has
been developed to determine methods that avoid alignments while
distributing the points uniformly. In sampling-based motion planning,
grids sometimes yield unexpected behavior because a row of points may
align nicely with a corridor in
![]() . In some cases, a solution
is obtained with surprisingly few samples, and in others, too many
samples are necessary. These alignment problems, when they exist,
generally drive the variance higher in computation times because it is
difficult to predict when they will help or hurt. This provides
motivation for developing sampling techniques that try to reduce this
sensitivity.
. In some cases, a solution
is obtained with surprisingly few samples, and in others, too many
samples are necessary. These alignment problems, when they exist,
generally drive the variance higher in computation times because it is
difficult to predict when they will help or hurt. This provides
motivation for developing sampling techniques that try to reduce this
sensitivity.
Discrepancy theory and its corresponding sampling methods were
developed to avoid these problems for numerical integration
[738]. Let ![]() be a measure space, such as
be a measure space, such as ![]() . Let
. Let
![]() be a collection of subsets of
be a collection of subsets of ![]() that is called a range
space. In most cases,
that is called a range
space. In most cases,
![]() is chosen as the set of all
axis-aligned rectangular subsets; hence, this will be assumed from
this point onward. With respect to a particular point set,
is chosen as the set of all
axis-aligned rectangular subsets; hence, this will be assumed from
this point onward. With respect to a particular point set, ![]() , and
range space,
, and
range space,
![]() , the discrepancy [965] for
, the discrepancy [965] for ![]() samples
is defined as (see Figure 5.7)
samples
is defined as (see Figure 5.7)
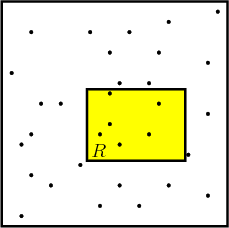 |