Relating dispersion and discrepancy

Since balls have positive volume, there is a close relationship between discrepancy, which is measure-based, and dispersion, which is metric-based. For example, for any $P \subset [0,1]^n$,

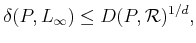$$\delta(P,L_\infty) \leq D(P,{\mathcal R})^{1/d},$$ (5.23)

which means low-discrepancy implies low-dispersion. Note that the converse is not true. An axis-aligned grid yields high discrepancy because of alignments with the boundaries of sets in ${\mathcal R}$, but the dispersion is very low. Even though low-discrepancy implies low-dispersion, lower dispersion can usually be obtained by ignoring discrepancy (this is one less constraint to worry about). Thus, a trade-off must be carefully considered in applications.