An approximate solution

First consider making a cell decomposition for the case in which the segment can only translate. The method from Section 4.3.2 can be used to compute ${\cal C}_{obs}$ by treating the robot-obstacle interaction with Type EV and Type VE contacts. When the interior of ${\cal A}$ touches an obstacle vertex, then Type EV is obtained. An endpoint of ${\cal A}$ touching an object interior yields Type VE. Each case produces an edge of ${\cal C}_{obs}$, which is polygonal. Once this is represented, the vertical decomposition can be used to solve the problem. This inspires a reasonable numerical approach to the rotational case, which is to discretize $\theta$ into $K$ values, $i \Delta \theta$, for $0 \leq i \leq K$, and $\Delta \theta = 2 \pi / K$ [20]. The obstacle region, ${\cal C}_{obs}$, is polygonal for each case, and we can imagine having a stack of $K$ polygonal regions. A roadmap can be formed by connecting sampling points inside of a slice in the usual way, and also by connecting samples between corresponding cells in neighboring slices. If $K$ is large enough, this strategy works well, but the method is not complete because a sufficient value for $K$ cannot be determined in advance. The method is actually an interesting hybrid between combinatorial and sampling-based motion planning. A resolution-complete version can be imagined.

In the limiting case, as $K$ tends to infinity, the surfaces of ${\cal C}_{obs}$ become curved along the $\theta$ direction. The conditions in Section 4.3.3 must be applied to generate the actual obstacle regions. This is possible, but it yields a semi-algebraic representation of ${\cal C}_{obs}$ in terms of implicit polynomial primitives. It is no easy task to determine an explicit representation in terms of simple cells that can be used for motion planning. The method of Section 6.3.3 cannot be used because ${\cal C}_{obs}$ is not polyhedral. Therefore, special analysis is warranted to produce a cell decomposition.

The general idea is to construct a cell decomposition in ${\mathbb{R}}^2$ by considering only the translation part, $(x,y)$. Each cell in ${\mathbb{R}}^2$ is then lifted into ${\cal C}$ by considering $\theta$ as a third axis that is ``above'' the $xy$ plane. A cylindrical decomposition results in which each cell in the $xy$ plane produces a cylindrical stack of cells for different $\theta$ values. Recall the cylinders in Figures 6.18 and 6.19. The vertical axis corresponds to $\theta$ in the current setting, and the horizontal axis is replaced by two axes, $x$ and $y$.

Figure 6.22: Fix $(x,y)$ and swing the segment around for all values of $\theta \in [0,2 \pi ]{/\sim }$. (a) Note the vertex and edge features that are hit by the segment. (b) Record orientation intervals over which the robot is not in collision.

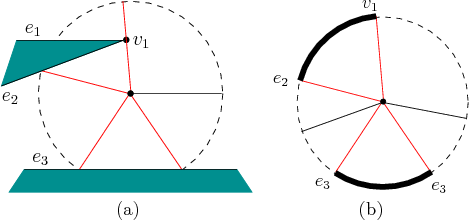To construct the decomposition in ${\mathbb{R}}^2$, consider the various robot-obstacle contacts shown in Figure 6.22. In Figure 6.22a, the segment swings around from a fixed $(x,y)$. Two different kinds of contacts arise. For some orientation (value of $\theta$), the segment contacts $v_1$, forming a Type EV contact. For three other orientations, the segment contacts an edge, forming Type VE contacts. Once again using the feature concept, there are four orientations at which the segment contacts a feature. Each feature may be either a vertex or an edge. Between the two contacts with $e_2$ and $e_3$, the robot is not in collision. These configurations lie in ${\cal C}_{free}$. Also, configurations for which the robot is between contacts $e_3$ (the rightmost contact) and $v_1$ are also in ${\cal C}_{free}$. All other orientations produce configurations in ${\cal C}_{obs}$. Note that the line segment cannot get from being between $e_2$ and $e_3$ to being between $e_3$ and $v_1$, unless the $(x,y)$ position is changed. It therefore seems sensible that these must correspond to different cells in whatever decomposition is made.