
Next: 6.3.3 3D Vertical Decomposition Up: 6.3.2 2D Decompositions Previous: Triangulation
The cylindrical decomposition is very similar to the vertical
decomposition, except that when any of the cases in Figure
6.2 occurs, then a vertical line slices through all
faces, all the way from
![]() to
to
![]() . The result
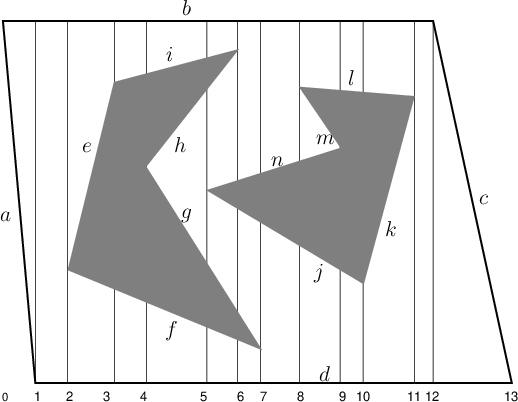
is shown in Figure 6.18, which may be considered as a
singular complex. This may appear very inefficient in comparison to
the vertical decomposition; however, it is presented here because it
generalizes nicely to any dimension, any C-space topology, and any
semi-algebraic model. Therefore, it is presented here to ease the
transition to more general decompositions. The most important
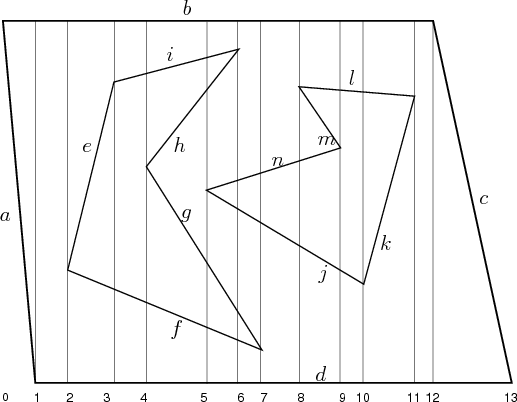
property of the cylindrical decomposition is shown in Figure
6.19. Consider each vertical strip between two events.
When traversing a strip from
. The result
is shown in Figure 6.18, which may be considered as a
singular complex. This may appear very inefficient in comparison to
the vertical decomposition; however, it is presented here because it
generalizes nicely to any dimension, any C-space topology, and any
semi-algebraic model. Therefore, it is presented here to ease the
transition to more general decompositions. The most important
property of the cylindrical decomposition is shown in Figure
6.19. Consider each vertical strip between two events.
When traversing a strip from ![]() to
to ![]() , the points
alternate between being
, the points
alternate between being
![]() and
and
![]() . For example, between
events
. For example, between
events ![]() and
and ![]() , the points below edge
, the points below edge ![]() are in
are in
![]() . Points
between
. Points
between ![]() and
and ![]() lie in
lie in
![]() . Points between
. Points between ![]() and
and ![]() lie in
lie in
![]() , and so forth. The cell decomposition can be defined so that
2D cells are also created in
, and so forth. The cell decomposition can be defined so that
2D cells are also created in
![]() . Let
. Let ![]() denote the logical
predicate (3.6) from Section
3.1.1. When traversing a strip, the value of
denote the logical
predicate (3.6) from Section
3.1.1. When traversing a strip, the value of ![]() also alternates. This behavior is the main reason to construct a
cylindrical decomposition, which will become clearer in Section
6.4.2. Each vertical strip is actually considered to be a
cylinder, hence, the name
cylindrical decomposition (i.e., there are not necessarily any
cylinders in the 3D geometric sense).
also alternates. This behavior is the main reason to construct a
cylindrical decomposition, which will become clearer in Section
6.4.2. Each vertical strip is actually considered to be a
cylinder, hence, the name
cylindrical decomposition (i.e., there are not necessarily any
cylinders in the 3D geometric sense).
 |
 |
Steven M LaValle 2020-08-14