Stevens' power law

Figure 2.22: Steven's power law (2.1) captures the relationship between the magnitude of a stimulus and its perceived magnitude. The model is an exponential curve, and the exponent depends on the stimulus type.

One of the most known results from psychophysics is Steven's power law, which characterizes the relationship between the magnitude of a physical stimulus and its perceived magnitude [316]. The hypothesis is that an exponential relationship occurs over a wide range of sensory systems and stimuli:

$$p = cm^x$$ (2.1)

in which

• $m$ is the magnitude or intensity of the stimulus,
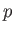• $p$ is the perceived magnitude,
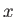• $x$ relates the actual magnitude to the perceived magnitude, and is the most important part of the equation, and
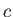• $c$ is an uninteresting constant that depends on units.

Note that for $x = 1$, (2.1) is a linear relationship, $p = cm$; see Figure 2.22. An example of this is our perception of the length of an isolated line segment directly in front of our eyes. The length we perceive is proportional to its actual length. The more interesting cases are when $x \not = 1$. For the case of perceiving the brightness of a target in the dark, $x = 0.33$, which implies that a large increase in brightness is perceived as a smaller increase. In the other direction, our perception of electric shock as current through the fingers yields $x = 3.5$. A little more shock is a lot more uncomfortable!