The Chen-Fliess-Sussmann equation

There are now two expressions for $\dot{S}$, which are given by (15.128) and (15.130). By equating them, $s$ equations of the form

$$\sum_{j=1}^s p_{j,k} {\dot z}_j = v_k$$ (15.131)

are obtained, in which $p_{j,k}$ is a polynomial in $z_i$ variables. This makes use of the series representation for each exponential; see Example 15.23.

The evolution of the backward P. Hall coordinates is therefore given by the Chen-Fliess-Sussmann (CFS) equation:

$${\dot z}= Q(z) v ,$$ (15.132)

in which $Q(z)$ is an $s \times s$ matrix, and $z(0) = 0$. The entries in $Q(z)$ are polynomials; hence, it is possible to integrate the system analytically to obtain expressions for the $z_i(t)$.

A simple example is given, which was worked out in [299]:

Example 15..23 (The CFS Equation for the Nonholonomic Integrator)   The extended system for the nonholonomic integrator was given in (15.115). The differential equation (15.128) for the Lie group is

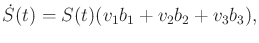$$\dot{S}(t) = S(t)(v_1 b_1 + v_2 b_2 + v_3 b_3),$$ (15.133)

because $s = 3$.

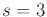
There are two expressions for its solution. The Chen-Fliess series (15.129) becomes

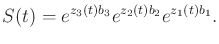$$S(t) = e^{z_3(t) b_3} e^{z_2(t) b_2} e^{z_1(t) b_1} .$$ (15.134)

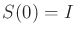
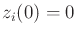
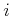
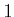
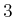
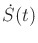
The initial condition $S(0) = I$ is satisfied if $z_i(0) = 0$ for $i$ from $1$ to $3$. The second expression for $\dot{S}(t)$ is (15.130), which in the case of the nonholonomic integrator becomes

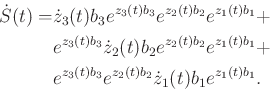$$\begin{split}\dot{S}(t) = & {\dot z}_3(t) b_3 e^{z_3(t) b_3} ... ...^{z_2(t) b_2} {\dot z}_1(t) b_1 e^{z_1(t) b_1} . \\ \end{split}$$ (15.135)

Note that

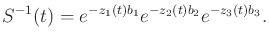$$S^{-1}(t) = e^{-z_1(t) b_1} e^{-z_2(t) b_2} e^{-z_3(t) b_3} .$$ (15.136)

Equating (15.133) and (15.135) yields

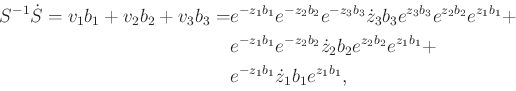$$\begin{split}S^{-1}\dot{S} = v_1 b_1 + v_2 b_2 + v_3 b_3 = & ... ..._1} + \\ & e^{-z_1 b_1} {\dot z}_1 b_1 e^{z_1 b_1}, \end{split}$$ (15.137)

in which the time dependencies have been suppressed to shorten the expression. The formal Lie series expansions, appropriately for the exponentials, are now used. For $i = 1, 2$,

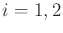
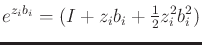$$e^{z_i b_i} = (I + z_i b_i + \begin{matrix}\frac{1}{2} \end{matrix} z_i^2 b_i^2)$$ (15.138)

and

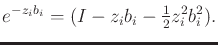$$e^{- z_i b_i} = (I - z_i b_i - \begin{matrix}\frac{1}{2} \end{matrix} z_i^2 b_i^2) .$$ (15.139)

Also,

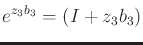$$e^{z_3 b_3} = (I + z_3 b_3)$$ (15.140)

and

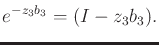$$e^{- z_3 b_3} = (I - z_3 b_3) .$$ (15.141)

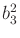
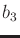
The truncation is clearly visible in (15.140) and (15.141). The $b_3^2$ terms are absent because $b_3$ is a polynomial of degree two, and its square would be of degree four.

Substitution into (15.137), performing noncommutative multiplication, and applying the Lie bracket definition yields

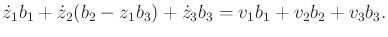$${\dot z}_1 b_1 + {\dot z}_2 (b_2 - z_1 b_3) + {\dot z}_3 b_3 = v_1 b_1 + v_2 b_2 + v_3 b_3 .$$ (15.142)

Equating like terms yields the Chen-Fliess-Sussmann equation

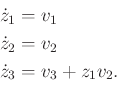$$\begin{split}{\dot z}_1 & = v_1 \\ {\dot z}_2 & = v_2 \\ {\dot z}_3 & = v_3 + z_1 v_2 . \\ \end{split}$$ (15.143)

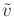
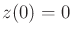
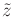
Recall that ${\tilde{v}}$ is given. By integrating (15.143) from $z(0) = 0$, the backward P. Hall coordinate trajectory ${\tilde{z}}$ is obtained. $\blacksquare$