
Next: The Chen-Fliess series Up: 15.5.1 Using the P. Previous: Formal calculations
The steering problem will be solved by performing calculations on
![]() . The formal power series of
. The formal power series of
![]() is the set of all linear combinations of
monomials, including those that have an infinite number of terms.
Similarly, the formal Lie series of
is the set of all linear combinations of
monomials, including those that have an infinite number of terms.
Similarly, the formal Lie series of
![]() can be
defined.
can be
defined.
The formal exponential map is defined for any
![]() as
as
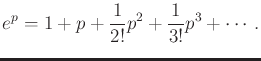 |
(15.116) |
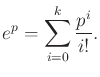 |
(15.117) |
A formal Lie group is constructed as
| (15.118) |
The following example is taken from [574]:
| (15.119) |
| (15.120) |
| (15.121) |
| (15.122) |
| (15.123) |
| (15.124) |
To be a group, the axioms given in Section 4.2.1
must be satisfied. The identity is ![]() , and associativity clearly
follows from the series representations. Each
, and associativity clearly
follows from the series representations. Each ![]() has an inverse,
has an inverse,
![]() , because
, because
![]() . The only remaining axiom to
satisfy is closure. This is given by the
Campbell-Baker-Hausdorff-Dynkin formula (or CBHD formula),
for which the first terms for any
. The only remaining axiom to
satisfy is closure. This is given by the
Campbell-Baker-Hausdorff-Dynkin formula (or CBHD formula),
for which the first terms for any
![]() are
are
The CBHD formula is often expressed as
Steven M LaValle 2020-08-14