
Next: 3.1.3 Other Models Up: 3.1 Geometric Modeling Previous: Polyhedral models
In both the polygonal and polyhedral models, ![]() was a linear
function. In the case of a semi-algebraic model for a 2D world,
was a linear
function. In the case of a semi-algebraic model for a 2D world, ![]() can be any polynomial with real-valued coefficients and variables
can be any polynomial with real-valued coefficients and variables ![]() and
and ![]() . For a 3D world,
. For a 3D world, ![]() is a polynomial with variables
is a polynomial with variables ![]() ,
, ![]() ,
and
,
and ![]() . The class of semi-algebraic models includes both polygonal
and polyhedral models, which use first-degree polynomials. A point
set determined by a single polynomial primitive is called an
algebraic set; a point set that can be obtained by a finite
number of unions and intersections of algebraic sets is called a
semi-algebraic set.
. The class of semi-algebraic models includes both polygonal
and polyhedral models, which use first-degree polynomials. A point
set determined by a single polynomial primitive is called an
algebraic set; a point set that can be obtained by a finite
number of unions and intersections of algebraic sets is called a
semi-algebraic set.
Consider the case of a 2D world. A solid representation can be defined using algebraic primitives of the form
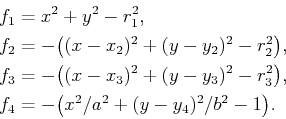 |
(3.11) |
In the case of semi-algebraic models, the intersection of primitives
does not necessarily result in a convex subset of ![]() . In general,
however, it might be necessary to form
. In general,
however, it might be necessary to form ![]() by taking unions and
intersections of algebraic primitives.
by taking unions and
intersections of algebraic primitives.
A logical predicate,
![]() , can once again be formed, and
collision checking is still performed in time that is linear in the
number of primitives. Note that it is still very efficient to
evaluate every primitive;
, can once again be formed, and
collision checking is still performed in time that is linear in the
number of primitives. Note that it is still very efficient to
evaluate every primitive; ![]() is just a polynomial that is evaluated
on the point
is just a polynomial that is evaluated
on the point ![]() .
.
The semi-algebraic formulation generalizes easily to the case of a 3D world. This results in algebraic primitives of the form
Equations (3.10) and (3.13) are sufficient
to express any model of interest. One may define many other
primitives based on different relations, such as
![]() ,
,
![]() ,
,
![]() ,
,
![]() , and
, and
![]() ; however, most of them do not enhance the set of models that can be
expressed. They might, however, be more convenient in certain
contexts. To see that some primitives do not allow new models to be
expressed, consider the primitive
; however, most of them do not enhance the set of models that can be
expressed. They might, however, be more convenient in certain
contexts. To see that some primitives do not allow new models to be
expressed, consider the primitive
Steven M LaValle 2020-08-14