To make a differential game against nature that extends Formulation 10.1 to
continuous time, suppose that nature actions 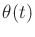 are chosen
from
are chosen
from 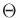 . A differential model can be defined as
. A differential model can be defined as
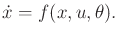 |
(13.199) |
The state space  and action space
and action space 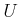 are used in the same way
as throughout this chapter. The difference only comes in the state
transition equation. State-dependent nature action spaces may also be
used.
are used in the same way
as throughout this chapter. The difference only comes in the state
transition equation. State-dependent nature action spaces may also be
used.
As observed repeatedly throughout Part III, nature can be
modeled nondeterministically or probabilistically. In the
nondeterministic case, (13.199) is equivalent to a
differential inclusion [53]:
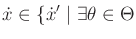 such that such that 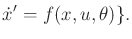 |
(13.200) |
Possible future values for 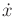 can be computed using forward
projections. Reachable sets, which will be introduced in Section
14.2.1, can be defined that characterize the evolution of
future possible states over time. Plans constructed under this model
usually use worst-case analysis.
can be computed using forward
projections. Reachable sets, which will be introduced in Section
14.2.1, can be defined that characterize the evolution of
future possible states over time. Plans constructed under this model
usually use worst-case analysis.
Example 13..15 (Nondeterministic Forward Projection)
As a simple example of using (
13.199), consider
expressing the uncertainty model used in the preimage planning
framework of Section
12.5.1.
At each time 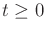 , nature chooses some
, nature chooses some
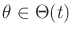 .
The state transition equation is
.
The state transition equation is
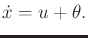 |
(13.201) |
The cone shown in Figure
12.45 is just the
nondeterministic forward projection under the application of a
constant
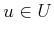
.

In the probabilistic case, restrictions must be carefully placed on
the nature action trajectory (e.g., a Weiner process
[910]). Under such conditions, (13.199)
becomes a stochastic differential equation. Planning in this
case becomes continuous-time stochastic control [567], and
the task is to optimize the expected cost.
Example 13..16 (A Simple Car and Nature)
Uncertainty can be introduced
into any of the models of this chapter. For example, recall the
simple car, (
13.15). Suppose that nature interferes with
the steering action so that it is not precisely known in which
direction the car will drive. Let
![$ \Theta =
[-\theta_{max},\theta_{max}]$](img6090.gif)
, in which
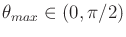
represents the maximum amount of steering angle error that can be
caused by nature. The simple-car model can be modified to account for
this error as
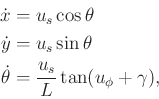 |
(13.202) |
in which the domain of
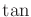
must be extended to
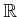
or other
suitable restrictions must be imposed. At each time
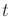
, a nature
action
13.12
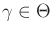
causes the true heading of
the car to be perturbed from the commanded direction
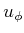
. Under
nondeterministic uncertainty, the maximum amount that the car deviates
from the commanded direction must be determined by the planning
algorithm. A probability density function
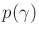
can be
assigned to obtain a probabilistic model. When integrated over time,
(
13.202) yields probability density functions over future
car configurations [
1004].

In a similar way, parameters that account for nature can be introduced
virtually anywhere in the models of this chapter. Some errors may be
systematic, which reflect mistakes or simplifications made in the
modeling process. These correspond to a constant nature action
applied at the outset. In this case, nature is not allowed to vary
its action over time. Other errors could correspond to noise, which is
expected to yield different nature actions over time.
Steven M LaValle
2020-08-14

![]() are chosen
from
are chosen
from ![]() . A differential model can be defined as
. A differential model can be defined as
![]() , nature chooses some
, nature chooses some
![]() .
The state transition equation is
.
The state transition equation is