- Consider the planning problem shown in Figure
2.21. Let
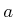 be the initial state, and let
be the initial state, and let 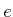 be
the goal state.
be
the goal state.
- [(a)] Use backward value iteration to determine the stationary cost-to-go.
- [(b)] Do the same but instead use forward value iteration.
Figure 2.21:
Another five-state discrete planning problem.
 |
- Try to construct a worst-case example for best-first search that
has properties similar to that shown in Figure 2.5, but
instead involves moving in a 2D world with obstacles, as introduced in
Example 2.1.
- It turns out that value iteration can be generalized
to a cost functional of the form
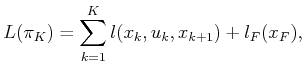 |
(2.41) |
in which
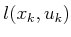 in (2.4) has been replaced by
in (2.4) has been replaced by
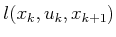 .
.
- Show that the dynamic programming principle can be applied in
this more general setting to obtain forward and backward value
iteration methods that solve the fixed-length optimal planning
problem.
- Do the same but for the more general problem of
variable-length plans, which uses termination conditions.
- The cost functional can be generalized to being stage-dependent, which means that the cost might depend on the
particular stage
 in addition to the state,
in addition to the state, 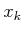 and the action
and the action
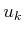 . Extend the forward and backward value iteration methods of
Section 2.3.1 to work for this case, and show that they give
optimal solutions. Each term of the more general cost functional
should be denoted as
. Extend the forward and backward value iteration methods of
Section 2.3.1 to work for this case, and show that they give
optimal solutions. Each term of the more general cost functional
should be denoted as
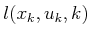 .
.
- Recall from Section 2.3.2 the method of defining a
termination action
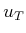 to make the value iterations work correctly
for variable-length planning. Instead of requiring that one remains
at the same state, it is also possible to formulate the problem by
creating a special state, called the terminal state,
to make the value iterations work correctly
for variable-length planning. Instead of requiring that one remains
at the same state, it is also possible to formulate the problem by
creating a special state, called the terminal state, 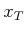 .
Whenever
.
Whenever 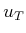 is applied, the state becomes
is applied, the state becomes 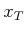 . Describe in
detail how to modify the cost functional, state transition equation,
and any other necessary components so that the value iterations
correctly compute shortest plans.
. Describe in
detail how to modify the cost functional, state transition equation,
and any other necessary components so that the value iterations
correctly compute shortest plans.
- Dijkstra's algorithm was presented as a kind of forward search
in Section 2.2.1.
- Develop a backward version of Dijkstra's algorithm that starts
from the goal. Show that it always yields optimal plans.
- Describe the relationship between the algorithm from part (a)
and the backward value iterations from Section 2.3.2.
- Derive a backward version of the
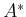 algorithm and show that
it yields optimal plans.
algorithm and show that
it yields optimal plans.
- Reformulate the general forward search algorithm of Section
2.2.1 so that it is expressed in terms of the STRIPS-like
representation. Carefully consider what needs to be explicitly
constructed by a planning algorithm and what is considered only
implicitly.
- Rather than using bit strings, develop a set-based formulation
of the logic-based planning problem. A state in this case can be
expressed as a set of positive literals.
- Extend Formulation 2.4 to allow disjunctive goal
sets (there are alternative sets of literals that must be satisfied).
How does this affect the binary string representation?
- Make a
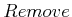 operator for Example 2.17 that
takes a battery away from the flashlight. For this operator to apply,
the battery must be in the flashlight and must not be blocked by
another battery. Extend the model to allow enough information for
the
operator for Example 2.17 that
takes a battery away from the flashlight. For this operator to apply,
the battery must be in the flashlight and must not be blocked by
another battery. Extend the model to allow enough information for
the 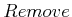 operator to function properly.
operator to function properly.
- Model the operation of the sliding-tile puzzle in Figure
1.1b using the STRIPS-like representation. You may use
variables in the operator definitions.
- Find the complete set of plans that are implicitly encoded by
Example 2.7.
- Explain why, in Formulation 2.4,
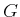 needs to include
both positive and negative literals, whereas
needs to include
both positive and negative literals, whereas 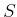 only needs positive
literals. As an alternative definition, could
only needs positive
literals. As an alternative definition, could 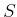 have contained only
negative literals? Explain.
have contained only
negative literals? Explain.
- Using Formulation 2.4,
model a problem in which a robot checks to determine whether a room is
dark, moves to a light switch, and flips on the light. Predicates
should indicate whether the robot is at the light switch and whether
the light is on. Operators that move the robot and flip the switch
are needed.
- Construct a planning graph for the model developed in Exercise
14.
- Express the model in Exercise 14 as a Boolean
satisfiability problem.
- In the worst case, how many terms are needed for the Boolean
expression for planning as satisfiability? Express your answer in
terms of
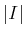 ,
, 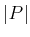 ,
, 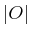 ,
, 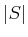 , and
, and 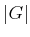 .
.
Implementations
- Using
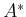 search, the performance
degrades substantially when there are many alternative solutions that
are all optimal, or at least close to optimal. Implement
search, the performance
degrades substantially when there are many alternative solutions that
are all optimal, or at least close to optimal. Implement 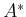 search
and evaluate it on various grid-based problems, based on Example
2.1. Compare the performance for two different cases:
search
and evaluate it on various grid-based problems, based on Example
2.1. Compare the performance for two different cases:
- Using
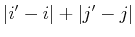 as the heuristic,
as suggested in Section 2.2.2.
as the heuristic,
as suggested in Section 2.2.2.
- Using
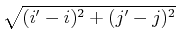 as the
heuristic.
as the
heuristic.
Which heuristic seems superior? Explain your answer.
- Implement
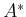 , breadth-first, and best-first search for
grid-based problems. For each search algorithm, design and
demonstrate examples for which one is clearly better than the other
two.
, breadth-first, and best-first search for
grid-based problems. For each search algorithm, design and
demonstrate examples for which one is clearly better than the other
two.
- Experiment with bidirectional search for grid-based planning.
Try to understand and explain the trade-off between exploring the state
space and the cost of connecting the trees.
- Try to improve the method used to solve Exercise
18 by detecting when the search might be caught in a
local minimum and performing random walks to try to escape. Try
using best-first search instead of
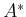 . There is great flexibility
in possible approaches. Can you obtain better performance on average
for any particular examples?
. There is great flexibility
in possible approaches. Can you obtain better performance on average
for any particular examples?
- Implement backward value iteration and verify its correctness by
reconstructing the costs obtained in Example 2.5.
Test the implementation on some complicated examples.
- For a planning problem under Formulation 2.3,
implement both Dijkstra's algorithm and forward value iteration.
Verify that these find the same plans. Comment on their differences
in performance.
- Consider grid-based problems for which there are mostly large,
open rooms. Attempt to develop a multi-resolution search algorithm
that first attempts to take larger steps, and only takes smaller steps
as larger steps fail. Implement your ideas, conduct experiments on
examples, and refine your approach accordingly.
Steven M LaValle
2020-08-14
