Critical gap events

As the robot moves, several important events can occur in the gap sensor:

1. Disappear: A gap disappears because the robot crosses an inflection ray as shown in Figure 12.28. This means that some previous shadow component is now visible.
2. Appear: A gap appears because the robot crosses an inflection ray in the opposite direction. This means that a new shadow component exists, which represents a freshly hidden portion of the environment.
3. Split: A gap splits into two gaps because the robot crosses a bitangent ray, as shown in Figure 12.29 (this was also shown in Figure 12.5). This means that one shadow component splits into two shadow components.
4. Merge: Two gaps merge into one because the robot crosses a bitangent ray in the oppose direction. In this case, two shadow components merge into one.

This is a complete list of possible events, under a general position assumption that precludes environments that cause degeneracies, such as three gaps that merge into one or the appearance of a gap precisely where two other gaps split.

Figure 12.28: (a) The robot crosses a ray that extends from an inflectional tangent. (b) A gap appears or disappears from the gap sensor, depending on the direction.

Figure 12.29: (a) The robot crosses a ray that extends from a bitangent. (b) Gaps split or merge, depending on the direction.

Figure 12.30: If a gap disappears, it is simply removed from the GNT.

Figure 12.31: If two gaps merge, an intermediate vertex is inserted into the tree.

Figure 12.32: If two gaps split, the intermediate vertex is removed.

Figure 12.33: The appearance of a gap results in a primitive vertex, which is denoted by a square.

As each of these gap events occurs, it needs to be reflected in the tree. If a gap disappears, as shown in Figure 12.30, then the corresponding edge and vertex are simply removed. If a merge event occurs, then an intermediate vertex is inserted as shown in Figure 12.31. This indicates that if that gap is chased, it will split into the two original gaps. If a split occurs, as shown in Figure 12.32, then the intermediate vertex is removed. The appearance of a gap is an important case, which generates a primitive vertex in the tree, as shown in Figure 12.33. Note that a primitive vertex can never split because chasing it will result in its disappearance.

Figure 12.34: A simple environment for illustrating the gap navigation tree.

Figure 12.35: Building a representation of the environment in Figure 12.34 using the gap navigation tree. The sequence is followed from left to right. For convenience, the ``R'' or ``L'' inside of each vertex indicates whether the shadow component is to the right or left of the gap, respectively. This information is not needed by the algorithm, but it helps in understanding the representation.

A simple example will now be considered.

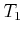
Example 12..6 (Gap Navigation Tree)   Suppose that the robot does not know the environment in Figure 12.34. It moves from cells 1 to 7 in order and then returns to cell 1. The following sequence of trees occurs: $T_1$, $\ldots$, $T_7$, $T'_6$, $\ldots$, $T'_1$, as shown in Figure 12.35. The root vertex is shown as a solid black disc. Vertices that are not known to be primitive are shown as circles; primitive vertices are squares. 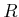Note that if any leaf vertex is a circle, then it means that the shadow region of $R$ that is hidden by that gap has not been completely explored. Note that once the robot reaches cell 5, it has seen the whole environment. This occurs precisely when all leaf vertices are primitive. When the robot returns to the first region, the tree is larger because it knows that the region on the right is composed of two smaller regions to the right. If all leaves are squares, this means that the environment has been completely explored. $\blacksquare$

Figure 12.36: Optimal navigation to a specified part of the environment is achieved by ``chasing'' the desired vertex in the GNT until it disappears. This will make a portion of the environment visible. In the example, the gap labeled ``h'' is chased.

In the example, all of the interesting parts of the environment were explored. From this point onward, all leaf vertices will be primitive vertices because all possible splits have been discovered. In a sense, the environment has been completely learned, at the level of resolution possible with the gap sensor. A simple strategy for exploring the environment is to chase any gaps that themselves are nonprimitive leaf vertices or that have children that are nonprimitive leaf vertices. A leaf vertex in the tree can be chased by repeatedly applying actions that chase its corresponding gap in the gap sensor. This may cause the tree to incrementally change; however, there is no problem if the action is selected to chase whichever gap hides the desired leaf vertex, as shown in Figure 12.36. Every nonprimitive leaf vertex will either split or disappear. After all nonprimitive leaf vertices have been chased, all possible splits have been performed and only primitive leaves remain. In this case, the environment has been completely learned.