The VisBug [666] and TangentBug
[505,592] strategies incorporate distance
measurements made by a range or visibility sensor to improve the
efficiency. The TangentBug strategy will be described here and is
illustrated in Figure 12.24. Suppose that in addition to
the sensors described previously, it is also equipped with a sensor
that produces measurements as shown in Figure 12.25. The
strategy is as follows:
- Move toward the goal, either through the
interior of the space or by wall following, until it is realized that
the robot is trapped in a local minimum or the goal is reached. This
is similar to the gradient-descent motion of the potential-field
planner of Section 5.4.3. If the goal is reached, then stop;
otherwise, go to the next step.
- Execute motions along the boundary. First, pick a direction by
comparing the previous heading to the goal direction. While moving
along the boundary, keep track of two distances:
 and
and  . The
distance
. The
distance  is the minimal distance from the goal, observed while
traveling along the boundary. The distance
is the minimal distance from the goal, observed while
traveling along the boundary. The distance  is the length of the
shortest path from the current position to the goal, assuming that the
only obstacles are those visible by the range sensor. The robot stops
following the boundary if
is the length of the
shortest path from the current position to the goal, assuming that the
only obstacles are those visible by the range sensor. The robot stops
following the boundary if  . In this case, go to Step
1. If the robot loops around the entire obstacle
without this condition occurring, then the algorithm reports that the
goal is not reachable.
. In this case, go to Step
1. If the robot loops around the entire obstacle
without this condition occurring, then the algorithm reports that the
goal is not reachable.
A one-parameter family of TangentBug algorithms can be made by setting
a depth limit for the range sensor. As the maximum depth is
decreased, the robot becomes more short-sighted and performance
degrades. It is shown in [505] that the distance
traveled is no greater than
 |
(12.27) |
in which 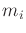 is the number of local minima for the
is the number of local minima for the 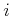 th
obstacle and
th
obstacle and 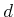 is the initial distance to the goal. The bound is
taken over
is the initial distance to the goal. The bound is
taken over 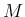 obstacles, which are assumed to intersect a disc of
radius
obstacles, which are assumed to intersect a disc of
radius 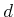 , centered at the goal (all others can be ignored). A
variant of the TangentBug, called WedgeBug, was developed in
[592] for planetary rovers that have a limited field of
view.
, centered at the goal (all others can be ignored). A
variant of the TangentBug, called WedgeBug, was developed in
[592] for planetary rovers that have a limited field of
view.
Steven M LaValle
2020-08-14

